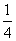题目内容
直线 过圆
过圆 的圆心,则
的圆心,则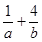 的最小值为 ( )
的最小值为 ( )
| A.8 | B.12 | C.16 | D.20 |
C
解析试题分析:把圆 化为
化为 ,其圆心为(-4,-1),∵直线
,其圆心为(-4,-1),∵直线 过圆心(-4,-1),∴4a+b=1,∴
过圆心(-4,-1),∴4a+b=1,∴ ,当且仅当
,当且仅当 时等号成立,故选C
时等号成立,故选C
考点:本题考查了直线与圆的位置关系及基本不等式的运用
点评:此题不能直接应用基本不等式,要注意“1”的代换,注意三个条件:正数、定值、等号成立的条件

练习册系列答案
相关题目
若 和
和 均为非零实数,则下列不等式中恒成立的是( )
均为非零实数,则下列不等式中恒成立的是( )
A. . . | B.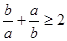 . . |
C.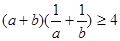 . . | D.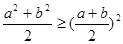 . . |
“a>b>0”是“ab< ”的 ( )
”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
若实数 、
、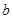 、
、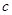 、
、 满足
满足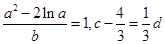 ,则
,则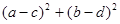 的最小值 为 ( )
的最小值 为 ( )
A.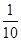 | B.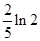 | C.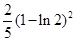 | D.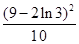 |
设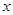 、
、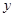 为正数,则
为正数,则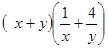 的最小值为( )
的最小值为( )
A.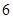 | B.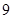 | C.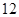 | D.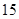 |
若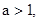 则
则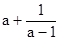 的最小值是 ( )
的最小值是 ( )
| A.2 | B.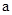 | C.3 | D.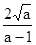 |
已知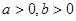 ,且函数
,且函数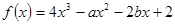 在
在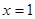 处有极值,则
处有极值,则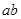 的最大值等于( )
的最大值等于( )
A.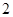 | B.3 | C.6 | D.9 |
已知 ,且
,且 ,则
,则 的最小值为( )
的最小值为( )
A. | B.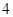 | C. | D.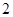 |
 、
、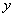 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) 1
1