题目内容
椭圆的一个顶点与两个焦点构成等边三角形，则离心率e=________．
分析：根据正三角形的性质可知b=
c，进而根据a，b和c的关系进而求得a和c的关系，则椭圆的离心率可得．解答：依题意可知b=
c∴a=
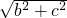=2c∴e=
=故答案为：
点评：本题主要考查了椭圆的简单性质．考查了学生对椭圆基础知识的把握和理解．
练习册系列答案
阅读快车系列答案
相关题目
椭圆的一个顶点与两个焦点构成等边三角形，则椭圆的离心率是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
B.
C.
D.