题目内容
已知曲线
的直角坐标方程为
. 以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系. P是曲线上一点，
，
，将点P绕点O逆时针旋转角
后得到点Q，
，点M的轨迹是曲线
.
（1）求曲线的极坐标方程；
（2）求
的取值范围.
（1）
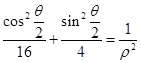；（2）[2，4].
解析试题分析：本题主要考查直角坐标方程与极坐标方程的互化、三角函数最值等基础知识，考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问，利用直角坐标方程和极坐标方程的转化公式“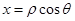
，
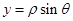”转化得到曲线的极坐标方程，设出M，P点的极坐标，利用已知条件得P点坐标代入到中即可；第二问，由曲线的极坐标方程得的表达式，利用三角函数的有界性求的最值.
（1）曲线C1的极坐标方程为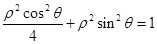
，即
．
在极坐标系中，设M(ρ，θ)，P(ρ1，α)，则
题设可知，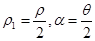
． ①
因为点P在曲线C1上，所以
． ②
由①②得曲线C2的极坐标方程为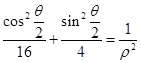． 6分
（2）由（1）得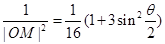
．
因为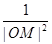
的取值范围是
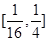，所以|OM|的取值范围是[2，4]． 10分
考点：直角坐标方程与极坐标方程的互化、三角函数最值.
练习册系列答案
相关题目
.
在该圆上，求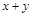
的最大值和最小值.
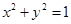上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C.
与C的交点为
，以坐标原点为极点，x轴正半轴为极坐标建立极坐标系，求过线段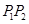
的中点且与
垂直的直线的极坐标方程.
的极坐标方程是
，以极点为原点，极轴为
轴正半轴，建立平面直角坐标系，两坐标系中取相同的长度单位.
作倾斜角为
的直线
与曲线
两点，求线段
的长度和
的值．
为极点，
轴的非负半轴为极轴建立极坐标系．已知曲线
的极坐标方程为
，直线
的参数方程为
（
为参数）．
在曲线
中，圆
的方程为
．以原点
为极点，以
轴正半轴为极轴，且与直角坐标系取相同的单位长度，建立极坐标系，直线
的极坐标方程为
．
(φ为参数),曲线C2的参数方程为
(a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=
时,这两个交点重合.
时,l与C1,C2的交点分别为A1,B1,当α=-
与圆
的交点坐标是__________.