题目内容
设函数f(x)=x2+bx-1(b∈R)
(1)当b=1时证明:f(x)在区间 内存在唯一零点;
内存在唯一零点;
(2)若当∈[1,2]时,不等式f(x)<1有解.求实数b的取值范围.
证明:(1)当b=1时,
f(x)=x2+x-1在区间 内单调递增
内单调递增
又∵f( )=
)= <0,f(1)=1>0
<0,f(1)=1>0
即f( )•f(1)<0
)•f(1)<0
∴f(x)在区间 内存在唯一零点;
内存在唯一零点;
(2)∵当x∈[1,2]时,不等式f(x)<1有解.
即x2+bx-1<1在[1,2]有解
即b<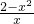 =
= -x在[1,2]有解
-x在[1,2]有解
∵g(x)= -x在[1,2]为减函数
-x在[1,2]为减函数
∴b<g(x)max=g(1)=1
∴实数b的取值范围为(-∞,1)
分析:(1)当b=1时,根据二次函数的性质易得f(x)在区间 内为增函数,进而根据f(
内为增函数,进而根据f( )•f(1)<0,可得f(x)在区间
)•f(1)<0,可得f(x)在区间 内存在唯一零点;
内存在唯一零点;
(2)若当∈[1,2]时,不等式f(x)<1有解,即b<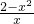 =
= -x在[1,2]有解,结合g(x)=
-x在[1,2]有解,结合g(x)= -x在[1,2]为减函数,可得b<g(x)max,进而得到答案.
-x在[1,2]为减函数,可得b<g(x)max,进而得到答案.
点评:本题考查的知识点是函数的零点,存在性问题,其中(1)的关键是分析出函数在区间 内为增函数及f(
内为增函数及f( )•f(1)<0,(2)的关键是将存在性问题转化为最值问题.
)•f(1)<0,(2)的关键是将存在性问题转化为最值问题.
f(x)=x2+x-1在区间
 内单调递增
内单调递增又∵f(
 )=
)= <0,f(1)=1>0
<0,f(1)=1>0即f(
 )•f(1)<0
)•f(1)<0∴f(x)在区间
 内存在唯一零点;
内存在唯一零点;(2)∵当x∈[1,2]时,不等式f(x)<1有解.
即x2+bx-1<1在[1,2]有解
即b<
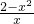 =
= -x在[1,2]有解
-x在[1,2]有解∵g(x)=
 -x在[1,2]为减函数
-x在[1,2]为减函数∴b<g(x)max=g(1)=1
∴实数b的取值范围为(-∞,1)
分析:(1)当b=1时,根据二次函数的性质易得f(x)在区间
 内为增函数,进而根据f(
内为增函数,进而根据f( )•f(1)<0,可得f(x)在区间
)•f(1)<0,可得f(x)在区间 内存在唯一零点;
内存在唯一零点;(2)若当∈[1,2]时,不等式f(x)<1有解,即b<
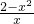 =
= -x在[1,2]有解,结合g(x)=
-x在[1,2]有解,结合g(x)= -x在[1,2]为减函数,可得b<g(x)max,进而得到答案.
-x在[1,2]为减函数,可得b<g(x)max,进而得到答案.点评:本题考查的知识点是函数的零点,存在性问题,其中(1)的关键是分析出函数在区间
 内为增函数及f(
内为增函数及f( )•f(1)<0,(2)的关键是将存在性问题转化为最值问题.
)•f(1)<0,(2)的关键是将存在性问题转化为最值问题. 
练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目