题目内容
已知向量 且
且 与
与 的夹角为锐角,则k的取值范围是 ( )
的夹角为锐角,则k的取值范围是 ( )A.(-2,+∞)
B.

C.(-∞,-2)
D.(-2,2)
【答案】分析:设  与
与 的夹角为锐角 θ,则由题意可得 cosθ>0,且
的夹角为锐角 θ,则由题意可得 cosθ>0,且 与
与 不平行,可得 k>2,且
不平行,可得 k>2,且  ,由此求得k的取值范围.
,由此求得k的取值范围.
解答:解:设 与
与 的夹角为锐角 θ,则由题意可得 cosθ=
的夹角为锐角 θ,则由题意可得 cosθ= =
= >0,且
>0,且 与
与 不平行.
不平行.
∴k>-2,且 ,解得 k>-2,且k≠
,解得 k>-2,且k≠ .
.
故k的取值范围是 ,
,
故选B.
点评:本题主要考查两个向量共线的性质,两个向量坐标形式的运算,两个向量夹角公式的应用,属于中档题.
 与
与 的夹角为锐角 θ,则由题意可得 cosθ>0,且
的夹角为锐角 θ,则由题意可得 cosθ>0,且 与
与 不平行,可得 k>2,且
不平行,可得 k>2,且  ,由此求得k的取值范围.
,由此求得k的取值范围.解答:解:设
 与
与 的夹角为锐角 θ,则由题意可得 cosθ=
的夹角为锐角 θ,则由题意可得 cosθ= =
= >0,且
>0,且 与
与 不平行.
不平行.∴k>-2,且
 ,解得 k>-2,且k≠
,解得 k>-2,且k≠ .
.故k的取值范围是
 ,
,故选B.
点评:本题主要考查两个向量共线的性质,两个向量坐标形式的运算,两个向量夹角公式的应用,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 且
且 与
与 的夹角为锐角,则
的夹角为锐角,则 的取值范围是( )
的取值范围是( ) B.
B. C .
C . D.
D.
 且
且 与
与 的夹角为锐角,则
的夹角为锐角,则 的取值范围是
的取值范围是 B.
B.

 D.
D.
 3
3 且
且 与
与 的夹角为
的夹角为 ,若向量
,若向量 与
与 的夹角为钝角,则实数k的取值范围是( )
的夹角为钝角,则实数k的取值范围是( ) B.
B. C.
C. D.
D.
 且
且 与
与 的夹角为钝角,则
的夹角为钝角,则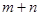 的取值范围是
的取值范围是 C.
C.  D. (2,6)
D. (2,6)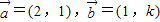 且
且 与
与 的夹角为锐角,则k的取值范围是 ( )
的夹角为锐角,则k的取值范围是 ( )