题目内容
已知数列{an}满足a1= ,且对任意n∈N*,都有
,且对任意n∈N*,都有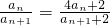 .
.
(Ⅰ)求证:数列 为等差数列;
为等差数列;
(Ⅱ)试问数列{an}中ak-ak+1(k∈N*)是否仍是{an}中的项?如果是,请指出是数列的第几项;如果不是,请说明理由.
(Ⅲ)令 ,证明:对任意n∈N*,都有不等式
,证明:对任意n∈N*,都有不等式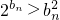 成立.
成立.
解:(Ⅰ)∵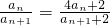
∴anan+1+2an=4anan+1+2an+1,
即2an-2an+1=3anan+1,
所以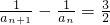
所以数列 是以
是以 为首项,公差为
为首项,公差为 的等差数列.
的等差数列.
(II)由(Ⅰ)可得数列 的通项公式为
的通项公式为 ,所以
,所以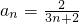
∴ =
=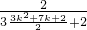 .
.
因为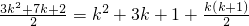
当k∈N*时, 一定是正整数,所以
一定是正整数,所以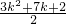 是正整数.
是正整数.
所以ak-ak+1是数列{an}中的项,是第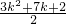 项.
项.
(Ⅲ)证明:由(II)知: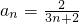 ,
,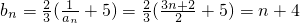 .
.
下面用数学归纳法证明:2n+4>(n+4)2对任意n∈N*都成立.
(1)当n=1时,显然25>52,不等式成立.
(2)假设当n=k(k∈N*)时,有2k+4>(k+4)2,
当n=k+1时,2(k+1)+4=2•2k+4>2(k+4)2=2k2+16k+32=(k+5)2+k2+6k+7>(k+5)2
即有: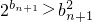 也成立.
也成立.
综合(i)(ii)知:对任意n∈N*,都有不等式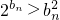 成立.
成立.
分析:(Ⅰ)条件可变形为anan+1+2an=4anan+1+2an+1,整理得2an-2an+1=3anan+1,两边同除以anan+1,可得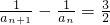 ,从而可得数列
,从而可得数列 是以
是以 为首项,公差为
为首项,公差为 的等差数列.
的等差数列.
(II)由(Ⅰ)可得数列 的通项公式为
的通项公式为 ,所以
,所以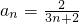 ,从而可得
,从而可得 =
=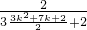 .只需证明
.只需证明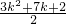 是正整数即可.
是正整数即可.
(Ⅲ)由(II)知: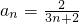 ,
,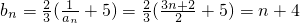 .下面用数学归纳法证明:2n+4>(n+4)2对任意n∈N*都成立.对于当n=k(k∈N*)时,有2k+4>(k+4)2,当n=k+1时,2(k+1)+4=2•2k+4>2(k+4)2=2k2+16k+32=(k+5)2+k2+6k+7>(k+5)2,从而可证.
.下面用数学归纳法证明:2n+4>(n+4)2对任意n∈N*都成立.对于当n=k(k∈N*)时,有2k+4>(k+4)2,当n=k+1时,2(k+1)+4=2•2k+4>2(k+4)2=2k2+16k+32=(k+5)2+k2+6k+7>(k+5)2,从而可证.
点评:本题以数列递推式为载体,考查等差数列的定义,考查不等式的证明,解题的关键是正确利用递推式求通项,掌握数学归纳法的证题步骤.
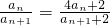
∴anan+1+2an=4anan+1+2an+1,
即2an-2an+1=3anan+1,
所以
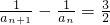
所以数列
 是以
是以 为首项,公差为
为首项,公差为 的等差数列.
的等差数列. (II)由(Ⅰ)可得数列
 的通项公式为
的通项公式为 ,所以
,所以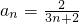
∴
 =
=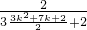 .
. 因为
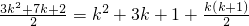
当k∈N*时,
 一定是正整数,所以
一定是正整数,所以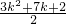 是正整数.
是正整数.所以ak-ak+1是数列{an}中的项,是第
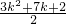 项.
项. (Ⅲ)证明:由(II)知:
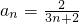 ,
,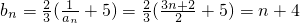 .
.下面用数学归纳法证明:2n+4>(n+4)2对任意n∈N*都成立.
(1)当n=1时,显然25>52,不等式成立.
(2)假设当n=k(k∈N*)时,有2k+4>(k+4)2,
当n=k+1时,2(k+1)+4=2•2k+4>2(k+4)2=2k2+16k+32=(k+5)2+k2+6k+7>(k+5)2
即有:
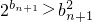 也成立.
也成立.综合(i)(ii)知:对任意n∈N*,都有不等式
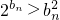 成立.
成立.分析:(Ⅰ)条件可变形为anan+1+2an=4anan+1+2an+1,整理得2an-2an+1=3anan+1,两边同除以anan+1,可得
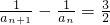 ,从而可得数列
,从而可得数列 是以
是以 为首项,公差为
为首项,公差为 的等差数列.
的等差数列. (II)由(Ⅰ)可得数列
 的通项公式为
的通项公式为 ,所以
,所以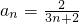 ,从而可得
,从而可得 =
=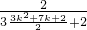 .只需证明
.只需证明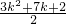 是正整数即可.
是正整数即可.(Ⅲ)由(II)知:
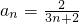 ,
,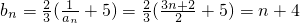 .下面用数学归纳法证明:2n+4>(n+4)2对任意n∈N*都成立.对于当n=k(k∈N*)时,有2k+4>(k+4)2,当n=k+1时,2(k+1)+4=2•2k+4>2(k+4)2=2k2+16k+32=(k+5)2+k2+6k+7>(k+5)2,从而可证.
.下面用数学归纳法证明:2n+4>(n+4)2对任意n∈N*都成立.对于当n=k(k∈N*)时,有2k+4>(k+4)2,当n=k+1时,2(k+1)+4=2•2k+4>2(k+4)2=2k2+16k+32=(k+5)2+k2+6k+7>(k+5)2,从而可证.点评:本题以数列递推式为载体,考查等差数列的定义,考查不等式的证明,解题的关键是正确利用递推式求通项,掌握数学归纳法的证题步骤.

练习册系列答案
相关题目