Question

已知正方体ABCD—A₁B₁C₁D₁,AA₁=2,E为棱CC₁的中点.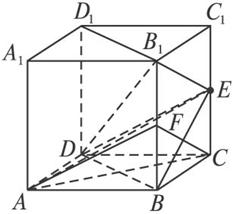

求证:(1)B₁D₁⊥AE;

(2)AC∥平面B₁DE.

Answer 1

证明：(1)连结BD,则BD∥B₁D₁,

∵ABCD是正方形,∴AC⊥BD.

∵CE⊥面ABCD,∴CE⊥BD.又AC∩CE=C,∴BD⊥面ACE.

∵AE面ACE,∴BD⊥AE.∴B₁D₁⊥AE.

(2)取BB₁的中点F,连结AF、CF、EF.∵E、F是CC₁、BB₁的中点,∴CEB₁F.

∴四边形B₁FCE是平行四边形.∴CF∥B₁E.

∵E、F是CC₁、BB₁的中点,∴EFBC.

又BCAD,∴EFAD.∴四边形ADEF是平行四边形.∴AF∥ED.

∵AF∩CF=F,B₁E∩ED=E,∴平面ACF∥面B₁DE.

又AC平面ACF,∴AC∥面B₁DE.