题目内容
在棱长为4的正方体ABCD-A1B1C1D1中，O是正方形A1B1C1D1的中心，点P在棱CC1上，且CC1=4CP．求点P到平面ABD1的距离；
解：方法一：“等积转换”．
如果直接研究三棱锥P-ABD1的体积，无论怎样“转换”都不易求；
在DD1上取一点Q，使DD1=4DQ，则PQ∥面ABD1，如图1；故VP-ABD1=VQ-ABD1，
记P到面ABD1的距离为h，则Q到面ABD1的距离为h，由VQ-ABD1=VB-QAD1得：h=
；
方法二：以D为原点建系，如图2，A（4，0，0），B（4，4，0），D1（0，0，4），
P（0，4，1），不难求出面ABD1的法向量
=（1，0，1），
=（4，0，-1），h=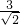
=；
方法三：“补齐”截面ABD1即正方体的对角面ABC1D1，过P作PE⊥BC1于E，如图3，
∵PE⊥AB，∴PE⊥面ABD1，∴PE的长度即为点P到平面ABD1的距离，易求PE=．
分析：方法一：如果直接研究三棱锥P-ABD1的体积，无论怎样“转换”都不易求可利用等体积法进行求解，在DD1上取一点Q，使DD1=4DQ，根据VP-ABD1=VQ-ABD1建立等式关系，求出所求即可；
方法二：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，求出面ABD1的法向量，然后求出在面ABD1的法向量上的射影即可；
方法三：“补齐”截面ABD1即正方体的对角面ABC1D1，过P作PE⊥BC1于E，根据线面垂直的性质可知PE的长度即为点P到平面ABD1的距离，最后求出PE的长即可．
点评：本题主要考查了点到平面的距离的求解，以及等体积法的应用等有关知识，考查空间想象能力和思维能力，应用向量知识解决立体几何问题的能力．
如果直接研究三棱锥P-ABD1的体积，无论怎样“转换”都不易求；
在DD1上取一点Q，使DD1=4DQ，则PQ∥面ABD1，如图1；故VP-ABD1=VQ-ABD1，
记P到面ABD1的距离为h，则Q到面ABD1的距离为h，由VQ-ABD1=VB-QAD1得：h=
；方法二：以D为原点建系，如图2，A（4，0，0），B（4，4，0），D1（0，0，4），
P（0，4，1），不难求出面ABD1的法向量
=（1，0，1），=（4，0，-1），h=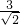=；方法三：“补齐”截面ABD1即正方体的对角面ABC1D1，过P作PE⊥BC1于E，如图3，
∵PE⊥AB，∴PE⊥面ABD1，∴PE的长度即为点P到平面ABD1的距离，易求PE=
．分析：方法一：如果直接研究三棱锥P-ABD1的体积，无论怎样“转换”都不易求可利用等体积法进行求解，在DD1上取一点Q，使DD1=4DQ，根据VP-ABD1=VQ-ABD1建立等式关系，求出所求即可；
方法二：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，求出面ABD1的法向量
，然后求出在面ABD1的法向量上的射影即可；方法三：“补齐”截面ABD1即正方体的对角面ABC1D1，过P作PE⊥BC1于E，根据线面垂直的性质可知PE的长度即为点P到平面ABD1的距离，最后求出PE的长即可．
点评：本题主要考查了点到平面的距离的求解，以及等体积法的应用等有关知识，考查空间想象能力和思维能力，应用向量知识解决立体几何问题的能力．
练习册系列答案
相关题目
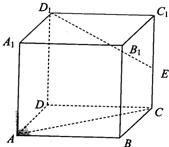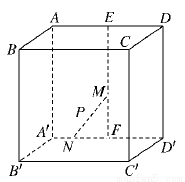
如图所示，在棱长为4的正方体ABCD-A1B1C1D1中，点E是棱CC1的中点．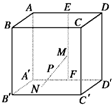
如图，在棱长为4的正方体ABCD-A′B′C′D′中，E、F分别是AD、A′D′的中点，长为2的线段MN的一个端点M在线段EF上运动，另一个端点N在底面A′B′C′D′上运动，则线段MN的中点P的轨迹（曲面）与二面角A-A′D′-B′所围成的几何体的体积为（ ）
在棱长为4的正方体ABCD-A1B1C1D1中，点E、F分别在棱AA1和AB上，且C1E⊥EF，则|AF|的最大值为（ ）
