题目内容
已知函数f(x)=x3+ax2+x+1,a∈R,
(Ⅰ)讨论函数f(x)的单调区间;
(Ⅱ)设函数f(x)在区间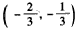 内是减函数,求a的取值范围。
内是减函数,求a的取值范围。
(Ⅰ)讨论函数f(x)的单调区间;
(Ⅱ)设函数f(x)在区间
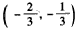 内是减函数,求a的取值范围。
内是减函数,求a的取值范围。 解:(Ⅰ)f′(x)=3x2+2ax+1,判别式△=4(a2-3),
(ⅰ)若 或
或 ,则在
,则在 上f′(x)>0,f(x)是增函数;
上f′(x)>0,f(x)是增函数;
在 内f′(x)<0,f(x)是减函数;
内f′(x)<0,f(x)是减函数;
在 上f′(x)>0,f(x)是增函数。
上f′(x)>0,f(x)是增函数。
(ⅱ)若 ,则对所有x∈R都有f′(x)>0,故此时f(x)在R上是增函数;
,则对所有x∈R都有f′(x)>0,故此时f(x)在R上是增函数;
(ⅲ)若 ,则
,则 ,且对所有的
,且对所有的 都有f′(x)>0,
都有f′(x)>0,
故当 时,f(x)在R上是增函数。
时,f(x)在R上是增函数。
(Ⅱ)由(Ⅰ)知,只有当 或
或 时,f(x)在
时,f(x)在 内是减函数,
内是减函数,
因此 ,①
,①
且 ,②
,②
当 时,由①②解得a≥2,
时,由①②解得a≥2,
因此a的取值范围是[2,+∞)。
(ⅰ)若
 或
或 ,则在
,则在 上f′(x)>0,f(x)是增函数;
上f′(x)>0,f(x)是增函数;在
 内f′(x)<0,f(x)是减函数;
内f′(x)<0,f(x)是减函数;在
 上f′(x)>0,f(x)是增函数。
上f′(x)>0,f(x)是增函数。(ⅱ)若
 ,则对所有x∈R都有f′(x)>0,故此时f(x)在R上是增函数;
,则对所有x∈R都有f′(x)>0,故此时f(x)在R上是增函数;(ⅲ)若
 ,则
,则 ,且对所有的
,且对所有的 都有f′(x)>0,
都有f′(x)>0,故当
 时,f(x)在R上是增函数。
时,f(x)在R上是增函数。(Ⅱ)由(Ⅰ)知,只有当
 或
或 时,f(x)在
时,f(x)在 内是减函数,
内是减函数,因此
 ,①
,①且
 ,②
,②当
 时,由①②解得a≥2,
时,由①②解得a≥2,因此a的取值范围是[2,+∞)。

练习册系列答案
相关题目