题目内容
(本题10分)在平面直角坐标系 中,已知抛物线
中,已知抛物线 :
: ,在此抛物线上一点N
,在此抛物线上一点N 到焦点的距离是3.
到焦点的距离是3.
(1)求此抛物线的方程;
(2)抛物线 的准线与
的准线与 轴交于
轴交于 点,过
点,过 点斜率为
点斜率为 的直线
的直线 与抛物线
与抛物线 交于
交于 、
、 两点.是否存在这样的
两点.是否存在这样的 ,使得抛物线
,使得抛物线 上总存在点
上总存在点 满足
满足 ,若存在,求
,若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)根据抛物线的定义列式即可求之;(2)根据题意设出直线方程,联立直线方程和抛物线方程 ,整理得
,整理得 ,假设存在直线与抛物线交于两点,可得
,假设存在直线与抛物线交于两点,可得 ,得
,得 且
且 ,由
,由 ,可得其斜率之积为-1,
,可得其斜率之积为-1, ,整理
,整理 ,此时应满足
,此时应满足 ,综上可得
,综上可得 且
且 .
.
试题解析:(1)抛物线准线方程是 ,
,
 ,
,
故抛物线的方程是 .
.
(2)设 ,
, ,
,
由 得
得 ,
,
由 得
得 且
且 .
.
 ,
,
 ,同理
,同理
由 得
得 ,
,
即: ,
,
∴ ,
,
 ,得
,得 且
且 ,
,
由 且
且 得,
得,
 的取值范围为
的取值范围为
考点:1、抛物线的定义;2、直线与抛物线的相交问题.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
下列各组对象不能构成一个集合的是( )
| A.不超过20的非负实数 |
B.方程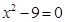 在实数范围内的解 在实数范围内的解 |
C. 的近似值的全体 的近似值的全体 |
| D.赣县中学北区2014年在校身高超过170厘米的同学 |
设全集U是实数集 ,
, ,
, 都是U的子集,则图中阴影部分所表示的集合是( )
都是U的子集,则图中阴影部分所表示的集合是( )
A.  | B. |
C. | D. |
 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 相切,则
相切,则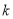 的取值范围是( )
的取值范围是( )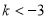 或
或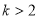
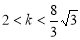
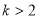 或
或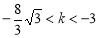
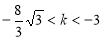 或
或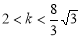

 ,
, 则
则
 ,
, ,
, ,那么
,那么 的大小关系为
的大小关系为 B.
B. C.
C. D.
D.
 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为直线
为直线 上一点,
上一点,
 是底角为
是底角为 的等腰三角形,则
的等腰三角形,则 的离心率为
的离心率为  >0,椭圆
>0,椭圆 的方程为
的方程为 ,双曲线
,双曲线 的方程为
的方程为 ,
, ,则
,则 的渐近线方程为( )
的渐近线方程为( ) B.
B. C.
C. D.
D.