Question

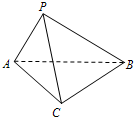（2013•临沂三模）如图，在三棱锥P-ABC中，∠APB=90°，∠PAB=60°，AB=BC=CA=PC．
（Ⅰ）求证：平面APB⊥平面ABC；
（Ⅱ）求二面角B-AP-C的余弦值．

Answer 1

分析：（I）过P作PO⊥AB，垂足为O，连结OC．设AB=2，在△AOC中，根据余弦定理算出OC=

13

2

，从而得出PO²+OC²=4=PC²，证出PO⊥OC，结合线面垂直判定定理得到PO⊥平面ABC，再由PO?平面APB，证出平面APB⊥平面ABC；
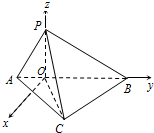
（II）以O为坐标原点，OB、OP所在直线为y轴、z轴，建立如图所示的空间直线坐标系，可得A、C、P各点的坐标，从而得到

AC

、

AP

的坐标，利用垂直向量数量积为零的方法建立方程组

n

=(1，-

3

，1)是平面APC的一个法向量．再由平面APB的向量为

m

=（1，0，0），算出

m

、

n

夹角的余弦值等于

5

5

，即可得到二面角B-AP-C的余弦值．

解答：解（Ⅰ）过P作PO⊥AB，垂足为O，连结OC．
设AB=2，则PA=1，AO=

1

2

，
在△AOC中，AO=

1

2

，AC=2，∠BAC=60°，
由余弦定理得OC=

AO2+AC2-2AO•ACcos60°

=

13

2

．
在△POC中，PO=

3

2

，OC=

13

2

，PC=2，
∴PO²+OC²=4=PC²，∴可得∠POC=90°，即PO⊥OC．
又∵PO⊥AB，且AB∩OC=O，∴PO⊥平面ABC
∵PO?平面APB，∴平面APB⊥平面ABC．
（Ⅱ）以O为坐标原点，OB、OP所在直线为y轴、z轴，建立如图所示的空间直线坐标系，
则可得A(0，-

1

2

，0)，C(

3

，

1

2

，0)，P(0，0，

3

2

)．
∴

AC

=(

3

，1，0)，

AP

=(0，

1

2

，

3

2

)，
设平面APC的一个法向量为

n

=（x₁，y₁，z₁），则

n • AC =0 n • AP =0

，即

3 x1+y1=0 1 2 y1+ 3 2 z1=0

令x₁=1，得y₁=-

3

，z₁=1，可得

n

=(1，-

3

，1)．
而平面APB的一个法向量为

m

=（1，0，0），设二面角B-AP-C的平面角为α，且α为锐角，
∴．cosα=

| n • m |

| n || m |

=

1

3+1+1

=

5

5

由此可得二面角B-AP-C的余弦值为

5

5

．

点评：本题在三棱锥中证明面面垂直，并且求二面角B-AP-C的余弦值．着重考查了线面垂直、面面垂直的判定定理和利用空间向量研究平面与平面所成角的大小的方法，属于中档题．