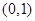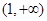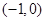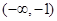题目内容
已知定义在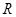 上的函数
上的函数 是周期为
是周期为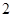 的偶函数,当
的偶函数,当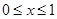 时,
时,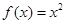 ,如果直线
,如果直线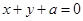 与曲线
与曲线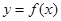 恰有两个交点,则实数
恰有两个交点,则实数 的值是( )
的值是( )
A. |
B.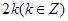 |
C.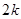 或 或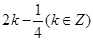 |
D.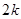 或 或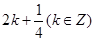 |
D
解析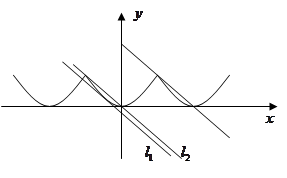
试题分析:由题意, 是偶函数,且当
是偶函数,且当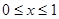 时,
时,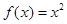 ,当
,当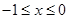 时,
时,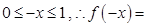
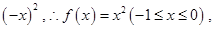 从而
从而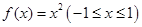 .
.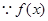 是周期为
是周期为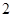 的偶函数,
的偶函数,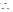 当
当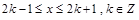 时,
时,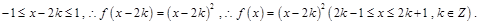
画出函数 的图像,满足线
的图像,满足线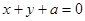 与曲线
与曲线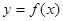 恰有两个交点,分两类情况:一是直线与一个周期内的抛物线弧相切,然后与另一个周期的抛物线弧相交一个交点,如
恰有两个交点,分两类情况:一是直线与一个周期内的抛物线弧相切,然后与另一个周期的抛物线弧相交一个交点,如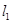 ,
,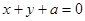 与
与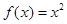 联立方程组,由判别式为0可得
联立方程组,由判别式为0可得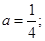 二是与抛物线有两个交点,如
二是与抛物线有两个交点,如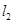 此时直线过原点,故
此时直线过原点,故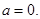 结合函数的周期为
结合函数的周期为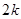 ,故答案为D.
,故答案为D.
考点:函数图象及其性质.

练习册系列答案
相关题目
设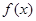 是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图像,则
是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图像,则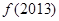 +
+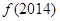 =( )
=( )
| A.3 | B.2 | C.1 | D.0 |
已知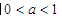 ,则函数
,则函数 的零点的个数为( )
的零点的个数为( )
| A.1 | B.2 | C.3 | D.4 |
函数f(x)=2x-sinx的零点个数为 ( )
| A.1 | B.2 | C.3 | D.4 |
若函数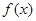 对任意的
对任意的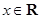 都有
都有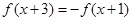 ,且
,且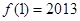 ,则
,则 ( )
( )
A.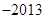 | B.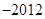 | C.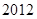 | D.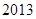 |
在平面直角坐标系中,横坐标和纵坐标均为整数的点称为格点,如果函数 的图象恰好通过
的图象恰好通过 个格点,则称函数
个格点,则称函数 为
为 阶格点函数. 给出下列4个函数:
阶格点函数. 给出下列4个函数:
① ;②
;② ;③
;③ ;④
;④ .
.
其中是一阶格点函数的是 ( )
| A.①③ | B.②③ | C.③④ | D.①④ |
设定义在 上的函数
上的函数 满足
满足 若
若 ,则
,则 ( )
( )
| A.13 | B.2 | C. | D. |
 满足
满足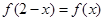 ,且在
,且在 上是减函数,
上是减函数,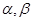 是钝角三角形的两个锐角,则下列不等式中正确的是( )
是钝角三角形的两个锐角,则下列不等式中正确的是( )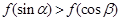
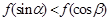

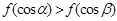
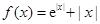 .若关于
.若关于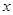 的方程
的方程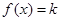 有两个不同的实根,则实数
有两个不同的实根,则实数 的取值范围是 ( )
的取值范围是 ( )