题目内容
如图，已知球O的球面上四点A，B，C，D，DA
平面ABC，AB
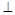BC，DA=AB=BC=
,
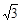则球O的表面积等于_____.
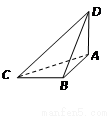
【答案】
【解析】
试题分析：由题意画出图形如图，因为三棱锥D-ABC的顶点都在球O的球面上，DA
平面ABC，AB
BC，DA=AB=BC=
,可知球的直径为
，因此其半径为
，那么可知球的表面积为，故答案为
考点：本题主要是考查直线与平面垂直的性质，球的内接几何体与球的关系，考查空间想象能力，计算能力．
点评：解决该试题的关键是画出图形，把三棱锥扩展为长方体，三棱锥的外接球就是长方体的外接球，长方体的体对角线就是球的直径，由此能求出球O的表面积．
练习册系列答案
相关题目
平面ABC，
，则球O的体积等于 。
，点A为球面上的一点，过点A作球O的截面圆O1，设截面圆O1的周长为x，球心O到截面圆O1的距离为y，当xy的值最大时，截面圆O1的面积是（ ）。