题目内容
若1<x≤2时,不等式ax2-2ax-1<0恒成立,求a的取值范围.
 解:设f(x)=ax2-2ax-1.
解:设f(x)=ax2-2ax-1.当a=0时,-1<0恒成立. …(3分)
当a≠0时,由f(x)的对称轴是x=1,结合二次函数的图象可知
当a>0时,只需
 可得a>0. …(7分)
可得a>0. …(7分)当a<0时,只需f(1)≤0,可得-1≤a<0.…(10分)
综上可得a≥-1.…(12分)
分析:由于二次项的系数为字母a,故需要a分a=0,a>0,a<0三类讨论,结合函数的单调性解决.
点评:本题考查二次函数的图象与性质,对a分a=0,a>0,a<0三类讨论,利用函数的单调性解决问题是关键,属于中档题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
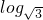 (x+a)的图象上.
(x+a)的图象上.