题目内容
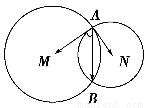
两个半径分别为r1,r2的圆M、N,公共弦AB长为3,如图所示,则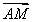 ·
·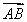 +
+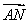 ·
·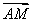 =________.
=________.
9
【解析】根据向量的数量积运算求解.连接圆心MN与公共弦相交于点C,则C为公共弦AB的中点,且MN⊥AB,故 ·
· =|
=| ||
|| |cos∠MAC=|
|cos∠MAC=| |·|
|·| |=
|= |
| |2=
|2= ,同理
,同理 ·
· =|
=| ||
|| |·cos∠NAC=|
|·cos∠NAC=| ||
|| |=
|= |
| |2=
|2= ,故
,故 ·
· +
+ ·
· =9.
=9.

练习册系列答案
相关题目
题目内容
两个半径分别为r1,r2的圆M、N,公共弦AB长为3,如图所示,则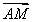 ·
·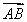 +
+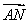 ·
·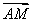 =________.
=________.

9
【解析】根据向量的数量积运算求解.连接圆心MN与公共弦相交于点C,则C为公共弦AB的中点,且MN⊥AB,故 ·
· =|
=| ||
|| |cos∠MAC=|
|cos∠MAC=| |·|
|·| |=
|= |
| |2=
|2= ,同理
,同理 ·
· =|
=| ||
|| |·cos∠NAC=|
|·cos∠NAC=| ||
|| |=
|= |
| |2=
|2= ,故
,故 ·
· +
+ ·
· =9.
=9.
