题目内容
已知函数f(x)=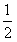 (1+x)2-ln(1+x),
(1+x)2-ln(1+x),
(1)求f(x)的单调区间;
(2)若x∈[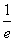 -1,e-1]时,f(x)<m恒成立,求m的取值范围.?
-1,e-1]时,f(x)<m恒成立,求m的取值范围.?
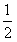 (1+x)2-ln(1+x),
(1+x)2-ln(1+x),(1)求f(x)的单调区间;
(2)若x∈[
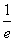 -1,e-1]时,f(x)<m恒成立,求m的取值范围.?
-1,e-1]时,f(x)<m恒成立,求m的取值范围.? 解:(1)∵f(x)=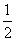 (1+x)2-ln(1+x),
(1+x)2-ln(1+x),
∴f′(x)=(1+x)-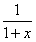 =
=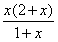 (x>-1),
(x>-1),
∴f(x)在(0,+∞)上单调递增,在(-1,0)上单调递减.
(2)令f′(x)=0,即x=0,则
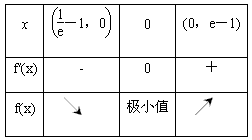
又∵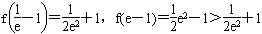 ,
,
又f(x)<m在x∈[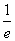 -1,e-1]上恒成立,
-1,e-1]上恒成立,
∴m>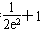 。
。
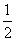 (1+x)2-ln(1+x),
(1+x)2-ln(1+x),∴f′(x)=(1+x)-
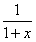 =
=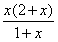 (x>-1),
(x>-1),∴f(x)在(0,+∞)上单调递增,在(-1,0)上单调递减.
(2)令f′(x)=0,即x=0,则

又∵
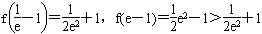 ,
,又f(x)<m在x∈[
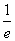 -1,e-1]上恒成立,
-1,e-1]上恒成立,∴m>
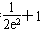 。
。
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|