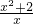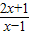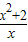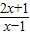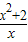题目内容
我们定义渐近线:已知曲线C,如果存在有一条直线,当曲线C上任一点M沿曲线运动时M可无限趋近于该直线但永远达不到,那么这条直线称为这条曲线的渐近线;下列函数:
①f(x)=x2+2x-3
②g(x)=2x+1
③h(x)=log2(x-1)
④t(x)=
⑤u(x)=
其中有渐近线的个数为( )
①f(x)=x2+2x-3
②g(x)=2x+1
③h(x)=log2(x-1)
④t(x)=
| 2x+1 |
| x-1 |
⑤u(x)=
| x2+2 |
| x |
其中有渐近线的个数为( )
分析:利用图象的变换规律,结合初等函数的图象特点,即可得到结论.
解答:解:①f(x)=x2+2x-3,根据渐近线的定义,不存在渐近线;
②g(x)=2x+1是由y=2x的图象向上平移1个单位得到,其渐近线方程为y=1;
③h(x)=log2(x-1)是由y=log2x向右平移一个单位得到,其渐近线方程为x=1;
④t(x)=
=2+
是由y=
向右平移1个单位,再向上平移2个单位,其渐近线方程为x=1,y=2;
⑤u(x)=
=x+
,其渐近线方程为x=0,y=x
综上,有渐近线的个数为4个
故选C.
②g(x)=2x+1是由y=2x的图象向上平移1个单位得到,其渐近线方程为y=1;
③h(x)=log2(x-1)是由y=log2x向右平移一个单位得到,其渐近线方程为x=1;
④t(x)=
| 2x+1 |
| x-1 |
| 3 |
| x-1 |
| 3 |
| x |
⑤u(x)=
| x2+2 |
| x |
| 2 |
| x |
综上,有渐近线的个数为4个
故选C.
点评:本题考查新定义,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
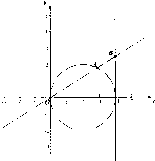 已知点A(x1,y1)在圆(x-2)2+y2=4上运动,点A不与(0,0)重合,点B(4,y0)在直线x=4上运动,动点M(x,y)满足
已知点A(x1,y1)在圆(x-2)2+y2=4上运动,点A不与(0,0)重合,点B(4,y0)在直线x=4上运动,动点M(x,y)满足