Question

函数f(x)=1-2a-2acosx-2sin²x的最小值为g(a),a∈R,

(1)求g(a);

(2)若g(a)=,求a及此时f(x)的最大值.

Answer 1

解:(1)f(x)=1-2a-2acosx-2(1-cos²x)

    =2cos²x-2acosx-1-2a

    =2(cosx-)²--2a-1.

    若＜-1,即a＜-2,则当cosx=-1时，

    f(x)有最小值g(a)=2(-1-)²--2a-1=1;

    若-1≤≤1,即-2≤a≤2,则当cosx=时,f(x)有最小值g(a)=--2a-1;

    若＞1，即a＞2,则当cosx=1时,f(x)有最小值g(a)=2(1-)²--2a-1=1-4a.

    ∴g(a)=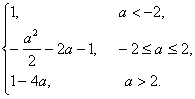  

    (2)若g(a)=,由所求g(a)的解析式知只能是--2a-1=或1-4a=.

    由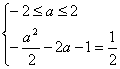

    a=-1或a=-3(舍).

    由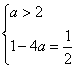a=(舍).

    此时f(x)=2(cosx+)²+,

    得f(x)_max=5.

    ∴若g(a)=,应a=-1,此时f(x)的最大值是5.