Question

设定义在R上的函数f （x）=ax⁴+a₁x³+a₂x²+a₃x （a_i∈R，i=0，1，2，3 ），当x=-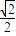时，f （x）取得极大值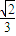，并且函数y=f（x）的图象关于y轴对称．
（1）求f （x）的表达式；
（2）试在函数f （x）的图象上求两点，使以这两点为切点的切线互相垂直，且切点的横坐标都在区间[-1，1]上；
（3）求证：|f （sin x）-f （cos x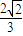）|≤（x∈R）．

Answer 1

【答案】分析：（1）先根据图象关于y轴对称，得其偶函数f（-x）=f（x），求得a=a₂=0，再利用导数研究单调性，列方程求得a₁和a₃，从而求f （x）的表达式；
（2）设所求两点的横坐标为x₁、x₂再利用切线的斜率之积为1：（2x₁²-1）（2x₂²-1）=-1，即可求得结果；
（3）因为|f（sinx）-f（cosx）|≤|f（sinx）|+|f（cosx）|，故欲求证：|f （sin x）-f （cos x）|≤（x∈R），只须探求|f（sinx）|和|f（cosx）|的取值范围即可，故只要利用导数研究函数f（x）的单调性即可．
解答：解：∵f（x）=4ax³+3a₁x²+2a₂x+a₃为偶函数，∴f（-x）=f（x），
∴-4ax³+3a₁x²-2a₂x+a₃=4ax³+3a₁x²+2a₂x+a₃，
∴4ax³+2a₂x=0对一切x∈R恒成立，
∴a=a₂=0，∴f（x）=a₁x³+a₃x
又当x=-时，f（x）取得极大值
∴解得
∴f（x）=x³-x．
（2）解：设所求两点的横坐标为x₁、x₂（x₁＜x₂），则（2x₁²-1）（2x₂²-1）=-1
又∵x₁，x₂∈[-1，1]，∴2x₁²-1∈[-1，1]，2x₂²-1∈[-1，1]
∴2x₁²-1，2x₂²-1中有一个为1，一个为-1，
∴或，
∴所求的两点为（0，0）与（1，-）或（0，0）与（-1，）．
（3）证明：易知sinx∈[-1，1]，cosx∈[-1，1]．
当0＜x＜时，f（x）＜0；当＜x＜1时，f（x）＞0．
∴f（x）在[0，]为减函数，在[，1]上为增函数，
又f（0）=0，f（）=-，f（1）=-，而f（x）在[-1，1]上为奇函数，
∴f（x）在[-1，1]上最大值为，最小值为-，即|f（x）|≤，
∴|f（sinx）|≤，|f（cosx）|≤，∴|f（sinx）-f（cosx）|≤|f（sinx）|+|f（cosx）|≤
点评：本题主要考查了待定系数法求函数解析式、不等式的证明、利用导数研究函数的单调性，属于中档题．