题目内容
在平面直角坐标系xoy中,已知圆心在直线y=x+4上,半径为 的圆C经过坐标原点O.
的圆C经过坐标原点O.
(1)求圆C的方程;
(2)是否存在直线l:x-y-m=0与圆C交于不同的两点A,B,且线段AB的中点恰在抛物线x2=4y上,若l存在,请求出m的值,若l不存在,请说明理由.
解:(1)由题意,设圆心坐标为(a,a+4)
∵半径为 的圆C经过坐标原点O
的圆C经过坐标原点O
∴a2+(a+4)2=8
∴a2+4a+4=0
∴a=-2
∴圆心坐标为(-2,2)
∴圆C的方程:(x+2)2+(y-2)2=8
(2)将直线l:x-y-m=0与圆C联立,消去y可得:2x2-2mx+m2+4m=0
设A(x1,y1),B(x2,y2),则x1+x2=m
∴y1+y2=x1+x2+2m=3m
∵线段AB的中点恰在抛物线x2=4y上
∴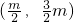 满足方程x2=4y
满足方程x2=4y
∴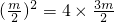
∴m=0或m=24
当m=0时,△=4m2-8(m2+4m)=0,不符合题意.
当m=24时,△=4m2-8(m2+4m)<0
所以不存在直线l:x-y-m=0与圆C交于不同的两点A,B,且线段AB的中点恰在抛物线x2=4y上
分析:(1)由题意,设圆心坐标为(a,a+4),利用半径为 的圆C经过坐标原点O,可得a2+(a+4)2=8,从而可得圆心坐标,进而可求圆C的方程;
的圆C经过坐标原点O,可得a2+(a+4)2=8,从而可得圆心坐标,进而可求圆C的方程;
(2)将直线l:x-y-m=0与圆C联立,消去y可得:2x2-2mx+m2+4m=0.设A(x1,y1),B(x2,y2),则x1+x2=m
,y1+y2=x1+x2+2m=3m,利用线段AB的中点恰在抛物线x2=4y上,可求得m=0或m=24,再验证△=4m2-8(m2+4m),即可知是否存在.
点评:本题考查的重点是圆的方程,考查直线与圆相交,解题时,将直线与圆联立是关键,判别式是否验证是易错点.
∵半径为
 的圆C经过坐标原点O
的圆C经过坐标原点O∴a2+(a+4)2=8
∴a2+4a+4=0
∴a=-2
∴圆心坐标为(-2,2)
∴圆C的方程:(x+2)2+(y-2)2=8
(2)将直线l:x-y-m=0与圆C联立,消去y可得:2x2-2mx+m2+4m=0
设A(x1,y1),B(x2,y2),则x1+x2=m
∴y1+y2=x1+x2+2m=3m
∵线段AB的中点恰在抛物线x2=4y上
∴
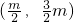 满足方程x2=4y
满足方程x2=4y∴
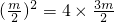
∴m=0或m=24
当m=0时,△=4m2-8(m2+4m)=0,不符合题意.
当m=24时,△=4m2-8(m2+4m)<0
所以不存在直线l:x-y-m=0与圆C交于不同的两点A,B,且线段AB的中点恰在抛物线x2=4y上
分析:(1)由题意,设圆心坐标为(a,a+4),利用半径为
 的圆C经过坐标原点O,可得a2+(a+4)2=8,从而可得圆心坐标,进而可求圆C的方程;
的圆C经过坐标原点O,可得a2+(a+4)2=8,从而可得圆心坐标,进而可求圆C的方程;(2)将直线l:x-y-m=0与圆C联立,消去y可得:2x2-2mx+m2+4m=0.设A(x1,y1),B(x2,y2),则x1+x2=m
,y1+y2=x1+x2+2m=3m,利用线段AB的中点恰在抛物线x2=4y上,可求得m=0或m=24,再验证△=4m2-8(m2+4m),即可知是否存在.
点评:本题考查的重点是圆的方程,考查直线与圆相交,解题时,将直线与圆联立是关键,判别式是否验证是易错点.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,一条渐近线方程为x-2y=0,则它的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.