题目内容
数列{an}的前n项和Sn满足:Sn=2an-3n(n∈N*).
(1)求数列{an}的通项公式an;
(2)数列{an}中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
(1)求数列{an}的通项公式an;
(2)数列{an}中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
解:(1)当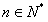 时,有
时,有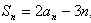 ,
,
∴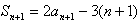 ,
,
两式相减,得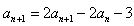 ,
,
∴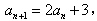
∴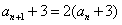 ,
,
又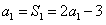 ,
,
∴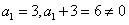 ,
,
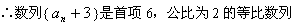 ,
,
从而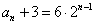 ,∴
,∴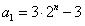 。
。
(2)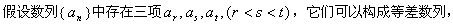
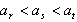 ,∴只能是
,∴只能是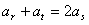 ,
,
∴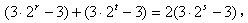
即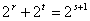 ,
,
∴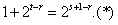 ,
,
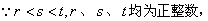
∴(*)式左边为奇数右边为偶数,不可能成立,
因此数列{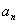 }中不存在可以构成等差数列的三项。
}中不存在可以构成等差数列的三项。
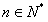 时,有
时,有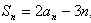 ,
,∴
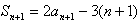 ,
,两式相减,得
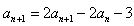 ,
,∴
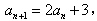
∴
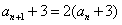 ,
,又
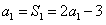 ,
,∴
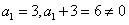 ,
,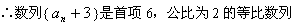 ,
,从而
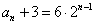 ,∴
,∴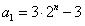 。
。(2)
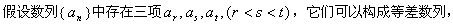
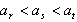 ,∴只能是
,∴只能是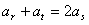 ,
,∴
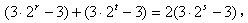
即
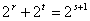 ,
,∴
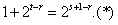 ,
,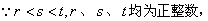
∴(*)式左边为奇数右边为偶数,不可能成立,
因此数列{
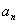 }中不存在可以构成等差数列的三项。
}中不存在可以构成等差数列的三项。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目