题目内容
已知f(x)=ax3+bx2+cx在区间[0,1]上是增函数,在区间(-∞,0),(1,+∞)上是减函数,又
(Ⅰ)求f(x)的解析式;
(Ⅱ)若在区间[0,m](m>0)上恒有f(x)≤x成立,求m的取值范围、
解:(Ⅰ)f'(x)=3ax2+2bx+c,由已知f'(0)=f'(1)=0,
即
解得
∴f'(x)=3ax2-3ax,
∴ ,
,
∴a=-2,
∴f(x)=-2x3+3x2.
(Ⅱ)令f(x)≤x,即-2x3+3x2-x≤0,
∴x(2x-1)(x-1)≥0,
∴ 或x≥1.
或x≥1.
又f(x)≤x在区间[0,m]上恒成立,
∴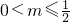 .
.
分析:(Ⅰ)由“f(x)在区间[0,1]上是增函数,在区间(-∞,0),(1,+∞)上是减函数”,则有f'(0)=f'(1)=0,再由
 求解.
求解.
(Ⅱ)首先将“f(x)≤x,x∈[0,m]成立”转化为“x(2x-1)(x-1)≥0,x∈[0,m]成立”求解.
点评:本题主要考查利用函数的极值点和导数值来求函数解析式及不等式恒成立问题.
即

解得

∴f'(x)=3ax2-3ax,
∴
 ,
,∴a=-2,
∴f(x)=-2x3+3x2.
(Ⅱ)令f(x)≤x,即-2x3+3x2-x≤0,
∴x(2x-1)(x-1)≥0,
∴
 或x≥1.
或x≥1.又f(x)≤x在区间[0,m]上恒成立,
∴
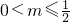 .
.分析:(Ⅰ)由“f(x)在区间[0,1]上是增函数,在区间(-∞,0),(1,+∞)上是减函数”,则有f'(0)=f'(1)=0,再由
 求解.
求解.(Ⅱ)首先将“f(x)≤x,x∈[0,m]成立”转化为“x(2x-1)(x-1)≥0,x∈[0,m]成立”求解.
点评:本题主要考查利用函数的极值点和导数值来求函数解析式及不等式恒成立问题.

练习册系列答案
相关题目
已知F(x)=ax3+bx5+cx3+dx-6,F(-2)=10,则F(2)的值为( )
| A、-22 | B、10 | C、-10 | D、22 |