题目内容
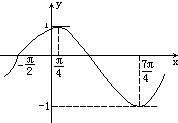 已知函数f(x)=Asin(ωx+?)(|φ|<
已知函数f(x)=Asin(ωx+?)(|φ|<| π | 2 |
(1)求f(x);
(2)求使f(x)取最小值的x的集合;
(3)f(x)的单调递增区间.
分析:(1)根据函数图象,得到A=1且函数周期T=3π,利用三角函数周期公式算出ω=
,再根据x=
时函数有最大值建立关于φ的等式,解之即可得到函数f(x)的表达式;
(2)根据三角函数最值的公式,解关于x的方程
x+
=-
+2kπ(k∈Z),即得使f(x)取最小值的x的集合;
(3)利用正弦函数的单调区间公式,建立关于x的不等式:-
+2kπ≤
x+
≤
+2kπ(k∈Z),解之即可得到f(x)的单调递增区间.
| 2 |
| 3 |
| π |
| 4 |
(2)根据三角函数最值的公式,解关于x的方程
| 2 |
| 3 |
| π |
| 3 |
| π |
| 2 |
(3)利用正弦函数的单调区间公式,建立关于x的不等式:-
| π |
| 2 |
| 2 |
| 3 |
| π |
| 3 |
| π |
| 2 |
解答:解:(1)由图象,可得A=1
函数的周期T=2(
-
)=3π,可得
=3π,ω=
又∵当x=
时函数有最大值
∴
•
+φ=
+2kπ(k∈Z),结合|φ|<
取k=0,得φ=
因此,函数的表达式为f(x)=sin(
x+
);
(2)令
x+
=-
+2kπ(k∈Z),可得x=-
+3kπ(k∈Z),
∴使f(x)取最小值的x的集合为{x|x=-
+3kπ,k∈Z};
(3)令-
+2kπ≤
x+
≤
+2kπ(k∈Z),
解得-
+3kπ≤x≤
+3kπ(k∈Z),
∴f(x)的单调递增区间为[-
+3kπ,
+3kπ](k∈Z).
函数的周期T=2(
| 7π |
| 4 |
| π |
| 4 |
| 2π |
| ω |
| 2 |
| 3 |
又∵当x=
| π |
| 4 |
∴
| 2 |
| 3 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
因此,函数的表达式为f(x)=sin(
| 2 |
| 3 |
| π |
| 3 |
(2)令
| 2 |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 4 |
∴使f(x)取最小值的x的集合为{x|x=-
| 5π |
| 4 |
(3)令-
| π |
| 2 |
| 2 |
| 3 |
| π |
| 3 |
| π |
| 2 |
解得-
| 5π |
| 4 |
| π |
| 4 |
∴f(x)的单调递增区间为[-
| 5π |
| 4 |
| π |
| 4 |
点评:本题给出函数y=Asin(ωx+φ)的部分图象,要求确定其解析式并讨论函数的单调区间与最值.着重考查了三角函数的图象与性质和确定三角函数解析式等知识,属于中档题.

练习册系列答案
相关题目