题目内容
已知圆C: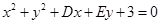 关于直线
关于直线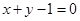 对称,圆心在第二象限,半径为
对称,圆心在第二象限,半径为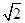
(1)求圆C的方程;
(2)是否存在斜率为2的直线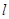 ,
,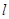 截圆C所得的弦为AB,且以AB为直径的圆过原点,若存在,则求出
截圆C所得的弦为AB,且以AB为直径的圆过原点,若存在,则求出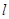 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
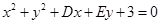 关于直线
关于直线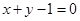 对称,圆心在第二象限,半径为
对称,圆心在第二象限,半径为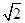
(1)求圆C的方程;
(2)是否存在斜率为2的直线
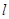 ,
,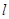 截圆C所得的弦为AB,且以AB为直径的圆过原点,若存在,则求出
截圆C所得的弦为AB,且以AB为直径的圆过原点,若存在,则求出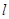 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.(1) (2)满足条件的直线不存在
(2)满足条件的直线不存在
 (2)满足条件的直线不存在
(2)满足条件的直线不存在试题分析:(1)圆心为
 2分
2分由题意:
 4分
4分解得:
 或
或 (舍)
(舍)圆C的方程为
 6分
6分(2)假设存在满足要求的直线
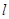 ,设其方程为
,设其方程为 ,
,设
 ,由题意,
,由题意, 8分
8分得:
 (*) 10分
(*) 10分将
 代入圆的方程
代入圆的方程 得:
得: ,该方程的两根为
,该方程的两根为 12分
12分将
 代入 (*)得:
代入 (*)得: 14分
14分 方程无解,满足条件的直线不存在. 16分
方程无解,满足条件的直线不存在. 16分点评:解决的关键是根据直线与圆的位置关系,结合韦达定理来求解分析,属于基础题。

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
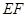 的长度为1,端点
的长度为1,端点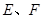 在边长为2的正方形
在边长为2的正方形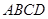 的四边上滑动.当
的四边上滑动.当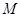 所形成的轨迹为
所形成的轨迹为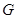 ,若
,若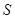 ,则
,则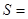 .
.
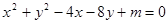 与
与 轴相切。
轴相切。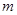 的值;
的值;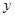 轴上截得的弦长;
轴上截得的弦长;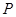 是直线
是直线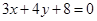 上的动点,过点
上的动点,过点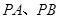 与圆M相切,
与圆M相切,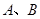 为切点。求四边形
为切点。求四边形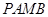 面积的最小值。
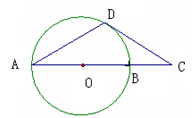
面积的最小值。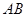 是圆O的直径,
是圆O的直径,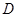 为圆O上一点,过
为圆O上一点,过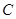 ,若DC=2,BC=1,则
,若DC=2,BC=1,则 .
.
 的圆的方程是 .
的圆的方程是 . 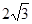 ,连接OC,CD⊥OC交⊙O于D,则CD的最大值为_____________.
,连接OC,CD⊥OC交⊙O于D,则CD的最大值为_____________.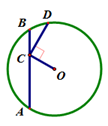
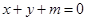 与圆
与圆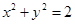 交于不同的两点A、B,O是坐标原点,且
交于不同的两点A、B,O是坐标原点,且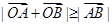 ,则实数m的取值范围是 。
,则实数m的取值范围是 。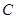 与定圆
与定圆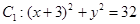 内切,与定圆
内切,与定圆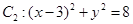 外切,A点坐标为
外切,A点坐标为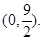 (1)求动圆
(1)求动圆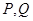 满足
满足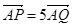 ,求
,求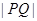 的值.
的值.