题目内容

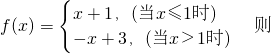$数学公式$ f[f（2）]=________．

解：∵2＞1，∴f（2）=-2+3=1，
∴f（1）=1+1=2．
∴f（f（2））=f（1）=2．
故答案为2．
分析：利用分段函数在不同区间上的解析式不同，将自变量代入相应的解析式即可．
点评：正确理解分段函数在不同区间上的对应法则不同是解题的关键．

练习册系列答案

快乐暑假江苏人民出版社系列答案

期末暑假衔接快乐驿站假期作业新疆青少年出版社系列答案

初中衔接教材浙江大学出版社系列答案

孟建平暑假培训教材浙江工商大学出版社系列答案

暑假作业安徽教育出版社系列答案

赢在暑假衔接教材合肥工业大学出版社系列答案

好学生系列衔接教材新疆美术摄影出版社系列答案

时刻准备着暑假作业原子能出版社系列答案

学生暑假实践手册北京出版社系列答案

新活力总动员寒假系列答案

相关题目

已知函数y=f（x），x∈N^*，y∈N^*满足：
①对于任意a，b∈N^*，a＜b，都有af（a）+bf（b）＞af（b）+bf（a）；
②对任意n∈N^*，都有f[f（n）]=3n．
（I）证明：f（x）为N^*上的单调增函数；
（II）求f（1），f（2），f（3）的值；
（III）令an=f(3n)，n∈N*，证明：

设f（x）在（0，+∞）上是单调递增函数，当n∈N^*时，f（n）∈N^*，且f[f（n）]=2n+1，则（　　）

A．f（1）=3，f（2）=4

B．f（1）=2，f（2）=3

C．f（2）=4，f（4）=5

D．f（2）=3，f（3）=4

已知函数y=f（x），x∈N^*，y∈N^*，满足：①对任意x1，x2∈N*，x1≠x2，都有x₁f（x₁）+x₂f（x₂）＞x₁f（x₂）+x₂f（x₁）；②对任意n∈N^*都有f[f（n）]=3n．
（1）试证明：f（x）为N^*上的单调增函数；
（2）求f（1）+f（6）+f（30）；
（3）令an=f(3n)，n∈N*，试证明：Sn=

，判断S_n与

的大小（不需要证明）

①函数y=f（-x+2）与y=f（x-2）的图象关于y轴对称；
②用二分法求函数f（x）=lnx+x-2在（1，2）上零点的近似值，要求精确度0.1，则至少需要五次对对应区间中点的函数值的计算；
③函数f（x）（其中f（x）恒不等于0）满足 f（x）=f（x+1）f（x-1），则f（2013）f（0）=1；
④若f（1-x）=-f（x+1），则函数y=f（x-1）的图象关于点（2，0）对称．
其中正确命题的序号是（　　）

若函数f（x）对定义域R内的任意x都有f（x）=f（2-x），且当x≠1时其导函数f′（x）满足xf′（x）＞f′（x），若1＜a＜2，则（　　）

A、f（2^a）＜f（2）＜f（log₂a）

B、f（log₂a）＜f（2）＜f（2^a）

C、f（2）＜f（log₂a）＜f（2^a）

D、f（log₂a）＜f（2^a）＜f（2）