题目内容
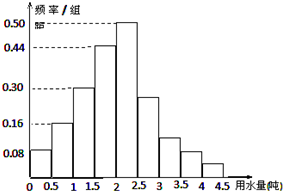 对某小区100户居民的月均用水量进行统计,得到样本的频率分布直方图,则估计此样本的众数、中位数分别为( )
对某小区100户居民的月均用水量进行统计,得到样本的频率分布直方图,则估计此样本的众数、中位数分别为( )| A、2.25,2.5 | B、2.25,2.02 | C、2,2.5 | D、2.5,2.25 |
分析:根据频率分布直方图,结合众数和中位数的定义进行求解即可.
解答:解:由频率分布直方图可知,数据在[2,2.5]之间的面积最大,此时众数集中在[2,2.5]内,用区间.2的中点值来表示,∴众数为2.25.
第一组的频率为0.08×0.5=0.05,对应的频数为0.05×100=5,
第二组的频率为0.16×0.5=0.08,对应的频数为0.08×100=8,
第三组的频率为0.30×0.5=0.15,对应的频数为0.15×100=15,
第四组的频率为0.44×0.5=0.22,对应的频数为0.22×100=22,
第五组的频率为0.50×0.5=0.25,对应的频数为0.25×100=25,
前四组的频数之和为5+8+15+22=50,
∴中位数为第4组的最后一个数据以及第5组的第一个数据,则对应的中位数在5组内且比2大一点,
故2.02比较适合,
故选:B.
第一组的频率为0.08×0.5=0.05,对应的频数为0.05×100=5,
第二组的频率为0.16×0.5=0.08,对应的频数为0.08×100=8,
第三组的频率为0.30×0.5=0.15,对应的频数为0.15×100=15,
第四组的频率为0.44×0.5=0.22,对应的频数为0.22×100=22,
第五组的频率为0.50×0.5=0.25,对应的频数为0.25×100=25,
前四组的频数之和为5+8+15+22=50,
∴中位数为第4组的最后一个数据以及第5组的第一个数据,则对应的中位数在5组内且比2大一点,
故2.02比较适合,
故选:B.
点评:本题考查频率分布直方图、利用频率分布直方图进行总体估计:求中位数以及众数的定义,比较基础.

练习册系列答案
相关题目
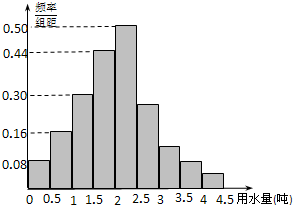 对某小区100户居民的月均用水量进行统计,得到样本的频率分布直方图,则估计此样本的众数是
对某小区100户居民的月均用水量进行统计,得到样本的频率分布直方图,则估计此样本的众数是