Question

如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD∥BC且AD＞BC,∠DAB=∠ABC=90°,PA=2,AB=BC=1,M为PC的中点.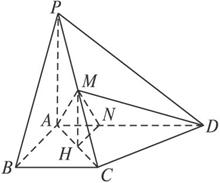

(1)求二面角M-AD-C的大小;

(2)如果∠AMD=90°,求线段AD的长.

Answer 1

解:(1)取AC的中点H,连结MH,则MH∥PA,所以MH⊥平面ABCD.过H作HN⊥AD于N,连结MN,可得MN⊥AD,则∠MNH就为所求的二面角的平面角.

AH=AC=,MH=PA=.在Rt△ANH中,HN=AN=AH=.

则在Rt△MHN中,tan∠MNH==.故所求的二面角的大小为arctan.

(2)若AM⊥MD,又因为PA=AC=,M为PC的中点,

则AM⊥PC,所以AM⊥平面PCD,则AM⊥CD.

AM在平面ABCD的射影为AH,可知其等价于AC⊥CD.

此时△ACD为等腰直角三角形,所以AD=AC=2.