题目内容
已知O为坐标原点,点A(2,1),B(1,2),对于k∈N*有向量 =k
=k +
+ ,
,
(1)试问点Pk是否在同一条直线上,若是,求出该直线的方程;若不是,请说明理由;
(2)是否在存在k∈N*使Pk在圆x2+(y-2)2=5上或其内部,若存在求出k,若不存在说明理由.
解:(1)点Pk(k∈N*)在同一条直线上,直线方程为y=2x-3.
证明如下:设Pk(xk,yk),则(xk,yk)=k(1,2)+(2,1),
∴ ,
,
∴yk=2xk-3.
∴点Pk在直线y=2x-3上.
(2)由圆x2+(y-2)2=5的圆心(0,2)到直线y=2x-3的距离为 =r,
=r,
可知直线与圆相切,∴直线与圆及内部最多只有一个公共点.
联立 解得
解得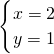 .
.
∴切点的坐标为:(2,1),此时k=0不满足题意,所以不存k∈N*满足题意.
分析:(1)利用向量的线性运算即可证明;
(2)先判断直线与圆的位置关系,进而即可得出结论.
点评:熟练掌握向量的线性运算和直线与圆的位置关系的判定方法是解题的关键.
证明如下:设Pk(xk,yk),则(xk,yk)=k(1,2)+(2,1),
∴
 ,
,∴yk=2xk-3.
∴点Pk在直线y=2x-3上.
(2)由圆x2+(y-2)2=5的圆心(0,2)到直线y=2x-3的距离为
 =r,
=r,可知直线与圆相切,∴直线与圆及内部最多只有一个公共点.
联立
 解得
解得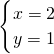 .
.∴切点的坐标为:(2,1),此时k=0不满足题意,所以不存k∈N*满足题意.
分析:(1)利用向量的线性运算即可证明;
(2)先判断直线与圆的位置关系,进而即可得出结论.
点评:熟练掌握向量的线性运算和直线与圆的位置关系的判定方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目