Question

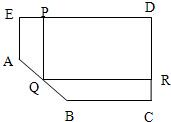为了绿化城市，准备在如图所示的区域ABCDE内修建一个矩形PQRD的草坪，其中∠AED=∠EDC=∠DCB=90°，点Q在AB上，且PQ∥CD，QR⊥CD，经测量BC=70m，CD=80m，DE=100m，AE=60m问应如何设计才能使草坪的占地面积最大？并求出最大面积（精确到1m²）．

Answer 1

分析：如图，先以BC边所在直线为x轴，，以AE边所在直线为y轴建立平面直角坐标系，求得直线AB的方程，再设出Q坐标，由矩形面积公式建立模型，然后根据函数的类型选择适当的方法求其最值．

解答：解：如图，以BC边所在直线为x轴，，以AE边所在直线为y轴建立平面直角坐标系，则A（0，20），B（30，0）．
所以直线AB的方程为：

x

30

+

y

20

=1，（4分）
即y=20-

2

3

x
设Q(x，20-

2x

3

)，则矩形PQRD的面
积为S=(100-x)[80-(20-

2x

3

)]
（0≤x≤30）（8分）
化简，得S=-

2

3

x2+

20

3

x+6000（0≤x≤30）
配方，S=-

2

3

(x-5)2+6000+

50

3

（0≤x≤30）（12分）
易得当x=5，y=

50

3

时，S最大，其最大值为Smax≈6017m²（14分）

点评：本题主要考查函数模型的建立和应用，主要涉及了用解析法解决平面问题，矩形面积公式，二次函数法求最值，以及数形结合的思想．