Question

如图,在三棱锥A—BCD中,∠BCD=90°,BC=CD=1 ,AB⊥平面BCD,∠ADB=60°,E、F分别是线段AC、AD上的动点,且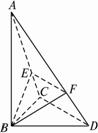＝λ(0＜λ＜1).

(1)求证:平面BEF⊥平面ABC.

(2)当λ为何值时,平面BEF⊥平面ACD?

Answer 1

(1)证明:∵AB⊥平面BCD,?

∴AB⊥CD.?

∵CD⊥BC,且AB∩BC=B,?

∴CD⊥平面ABC.?

又∵=λ(0＜λ＜1),?

∴EF∥CD.?

∴EF⊥平面ABC,EF平面BEF.?

∴平面BEF⊥平面ABC.?

(2)证明:由(1)知BE⊥EF,又平面BEF⊥平面ACD,?

∴BE⊥平面ACD.∴BE⊥AC.?

∵BC=CD=1,∠BCD=90°,∠ADB=60°,∴BD=,AB=tan60°=.?

∴AC=.?

由AB²=AE·AC,得AE=.?

∴λ=.故当λ=时,平面BEF⊥平面ACD.