Question

已知函数f（x）=2ax³-3ax²+1，g（x）=-

a

4

x+

3

2

，（a＜0），若对任意给定的x₀∈[-1，

5

4

]，在区间[-1，

5

4

]上总存在唯一一个x₁，使得f（x₁）=g（x₀）成立，则a的取值范围为（　　）

• A．-2≤a≤-

  8

  75

• B．-

  2

  5

  ＜a≤-

  8

  75

• C．-2＜a＜-

  16

  15

• D．-

  16

  15

  ＜a＜-

  2

  5

Answer 1

分析：求出原函数的导函数，列表分析出函数f（x）在[-1，

5

4

]上的取值情况，并且由表中数值看出，只有当f（x）的取值在（1-a，1-5a]时，一个函数值对应一个自变量的值，然后由g（x）的单调性求出g（x）的值域，由g（x）的值域是（1-a，1-5a]的子集列式求解a的取值范围．

解答：解：当a＜0时，f'（x）=6ax²-6ax=6ax（x-1）．

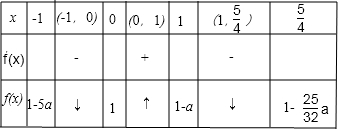
由表可知，当f（x）∈（1-a，1-5a]时，x与f（x）是一一对应关系．
又∵当a＜0时，g（x）=-

a

4

x+

3

2

在[-1，

5

4

]上是增函数，
∴对任意x∈[-1，

5

4

]，g（x）∈[

a+6

4

，

24-5a

16

]．
则

a+6 4 ＞1-a 24-5a 16 ≤1-5a

，解得：-

2

5

＜a≤-

8

75

．
∴a的取值范围为-

2

5

＜a≤-

8

75

．
故选：B．

点评：本题考查了函数在某点取得极值的条件，训练了利用函数单调性求函数的值域，考查了数学转化思想方法，解答的关键是把问题转化为两个集合之间的关系，是中档题．