题目内容
设f(x)=ex-ax-1
(1)若f(x)在[-∞,0]上单调递减,在[0,+∞]上单调递增,求实数a的取值范围;
(2)设g(x)=-x2+2x-2,在(1)的条件下,求证:g(x)的图象恒在f(x)图象的下方.
(1)若f(x)在[-∞,0]上单调递减,在[0,+∞]上单调递增,求实数a的取值范围;
(2)设g(x)=-x2+2x-2,在(1)的条件下,求证:g(x)的图象恒在f(x)图象的下方.
分析:(1)利用函数的单调性,可得f′(0)=0,即可求实数a的取值范围;
(2)只需证明f(x)min>g(x)max,即可得到结论.
(2)只需证明f(x)min>g(x)max,即可得到结论.
解答:(1)解:求导数可得f′(x)=ex-a
∵f(x)在(-∞,0]上单调递减,在[0,+∞)上单调递增,
∴f′(0)=e0-a=0,
∴a=1;
(2)证明:由(1)知,f(x)min=0
∵g(x)=-x2+2x-2=-(x-1)2-1,∴x=1时,g(x)max=-1
∵f(x)min>g(x)max,
∴g(x)的图象恒在f(x)图象的下方.
∵f(x)在(-∞,0]上单调递减,在[0,+∞)上单调递增,
∴f′(0)=e0-a=0,
∴a=1;
(2)证明:由(1)知,f(x)min=0
∵g(x)=-x2+2x-2=-(x-1)2-1,∴x=1时,g(x)max=-1
∵f(x)min>g(x)max,
∴g(x)的图象恒在f(x)图象的下方.
点评:本题考查函数的单调性,考查函数的最值,考查学生的计算能力,属于中档题.

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
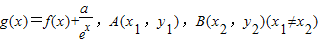 是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;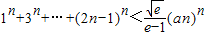 对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.
对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由. 是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;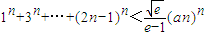 对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.
对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.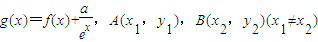 是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;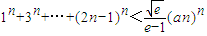 对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.
对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.