题目内容
已知函数f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若m,n∈[-1,1],m+n≠0时,有 ,若f(x)≤t2-2at+1对所有x∈[-1,1],t∈[0,1]恒成立,则实数a的取值范围是________.
,若f(x)≤t2-2at+1对所有x∈[-1,1],t∈[0,1]恒成立,则实数a的取值范围是________.
(-∞,0]
分析:先由单调性定义判断和证明f(x)在[-1,1]上为增函数,从而求得f(x)的最大值,再转化为关于a的不等式恒成立问题求解.
解答:任取-1≤x1<x2≤1,则
f(x1)-f(x2)=f(x1)+f(-x2)=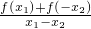 •(x1-x2)
•(x1-x2)
∵-1≤x1<x2≤1,∴x1+(-x2)≠0,
由已知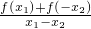 >0,又x1-x2<0,
>0,又x1-x2<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
所以f(x)在[-1,1]上为增函数.
∵f(1)=1,∴对x∈[-1,1],恒有f(x)≤1.
所以要使f(x)≤t2-2at+1对所有x∈[-1,1],t∈[0,1]恒成立,
即要t2-2at+1≥1成立,故t2-2at≥0成立.
∵t∈[0,1],
∴t≠0时2a≤t,即a≤ ,解得a∈(-∞,0].
,解得a∈(-∞,0].
t=0时,a∈R,
综上,a∈(-∞,0].
故答案为:(-∞,0].
点评:本题主要考查单调性和奇偶性的综合应用及函数最值、恒成立问题的转化化归思想.
分析:先由单调性定义判断和证明f(x)在[-1,1]上为增函数,从而求得f(x)的最大值,再转化为关于a的不等式恒成立问题求解.
解答:任取-1≤x1<x2≤1,则
f(x1)-f(x2)=f(x1)+f(-x2)=
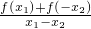 •(x1-x2)
•(x1-x2)∵-1≤x1<x2≤1,∴x1+(-x2)≠0,
由已知
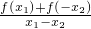 >0,又x1-x2<0,
>0,又x1-x2<0,∴f(x1)-f(x2)<0,即f(x1)<f(x2),
所以f(x)在[-1,1]上为增函数.
∵f(1)=1,∴对x∈[-1,1],恒有f(x)≤1.
所以要使f(x)≤t2-2at+1对所有x∈[-1,1],t∈[0,1]恒成立,
即要t2-2at+1≥1成立,故t2-2at≥0成立.
∵t∈[0,1],
∴t≠0时2a≤t,即a≤
 ,解得a∈(-∞,0].
,解得a∈(-∞,0].t=0时,a∈R,
综上,a∈(-∞,0].
故答案为:(-∞,0].
点评:本题主要考查单调性和奇偶性的综合应用及函数最值、恒成立问题的转化化归思想.

练习册系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+