题目内容
设向量![]() ,点
,点![]() 为动点,已知
为动点,已知![]() ,且点P的轨迹C1。若抛物线C2的顶点在原点,与轨迹C1共焦点F,设抛物线C2与轨迹C1的交点分别为M、N。
,且点P的轨迹C1。若抛物线C2的顶点在原点,与轨迹C1共焦点F,设抛物线C2与轨迹C1的交点分别为M、N。
(1)分虽求轨迹为C1与抛物线C2的方程;
(2)过F作一条与![]() 轴不垂直的直线,与曲线C1在点M、N左侧的部分交于C、D两点,与曲线C2在点M、N左侧的部分交于B、E两点,若G为CD的中点,H为BE的中点,问
轴不垂直的直线,与曲线C1在点M、N左侧的部分交于C、D两点,与曲线C2在点M、N左侧的部分交于B、E两点,若G为CD的中点,H为BE的中点,问 是否为定值?若是,求出定值;若不是,请说明理由。
是否为定值?若是,求出定值;若不是,请说明理由。
(1) ![]() (2)
(2) ![]()
解析:
(1)![]() 6分
6分
(2)设![]() ,
,
直线![]() ,
,
将直线![]() 代入
代入![]()
得:![]() ,
,
由韦达定理: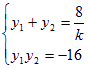
同理,将![]() ,
,
代入![]() 得:
得:![]()
即![]() ,
,
由韦达定理: 9分
9分



![]()
 为定值。 12分
为定值。 12分

练习册系列答案
相关题目
 ,点
,点 为动点,
为动点, 已知
已知 。
。 的轨迹方程;
的轨迹方程; 轴负半轴交于点
轴负半轴交于点 ,过点
,过点 的直线交点
的直线交点 的轨迹于
的轨迹于 、
、 两点,试推断
两点,试推断 的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由。
的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由。 ,点
,点 为动点,
为动点, 已知
已知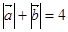 。
。 的轨迹方程;
的轨迹方程; 轴负半轴交于点
轴负半轴交于点 ,过点
,过点 的直线交点
的直线交点 的轨迹于
的轨迹于 、
、 两点,试推断
两点,试推断 的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由。
的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由。 ,点
,点 为动点,
为动点, 已知
已知 。
。 的轨迹方程;
的轨迹方程; 轴负半轴交于点
轴负半轴交于点 ,过点
,过点 的直线交点
的直线交点 的轨迹于
的轨迹于 、
、 两点,试推断
两点,试推断 的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由。
的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由。 ,点
,点 为动点,
为动点, 已知
已知 。
。 的轨迹方程;
的轨迹方程; 轴负半轴交于点
轴负半轴交于点 ,过点
,过点 的直线交点
的直线交点 的轨迹于
的轨迹于 、
、 两点,试推断
两点,试推断 的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由。
的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由。