题目内容
在△ABC中，a，b，c分别为角A，B，C所对的三边，a2﹣（b﹣c）2=bc，
（1）求角A；
（2）若BC=2
，角B等于x，周长为y，求函数y=f（x）的取值范围．
（1）求角A；
（2）若BC=2
，角B等于x，周长为y，求函数y=f（x）的取值范围．解：（Ⅰ）∵a2﹣（b﹣c）2=bc
∴a2﹣b2﹣c2=﹣bc
∴cosA=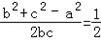
又0＜A＜π
∴A=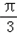
（Ⅱ)∵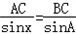
∴AC=
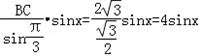
同理AB=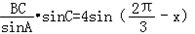
∴y=4sinx+4sin（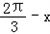
）+2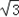
=
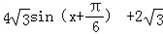
∵A=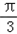
∴0＜B=x＜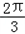
故x+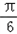
∈（
），
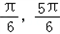∴sin（x+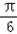
）∈（
，1]∴y∈（4
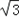，6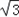
]．
∴a2﹣b2﹣c2=﹣bc
∴cosA=
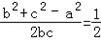又0＜A＜π∴A=
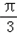
（Ⅱ)∵
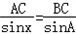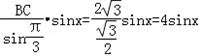
∴AC=同理AB=
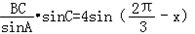
∴y=4sinx+4sin（
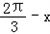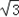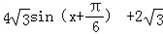
）+2=∵A=
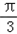∴0＜B=x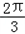＜故x+
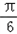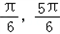∈（），∴sin（x+
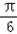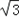）∈（，1]∴y∈（4，6]．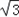
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，∠A、∠B、∠C所对的边长分别是a、b、c．满足2acosC+ccosA=b．则sinA+sinB的最大值是（ ）
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|