题目内容
(本小题满分14分)
(1)已知等差数列{an}的前n项和为Sn,若m+n=s+t(m,n,s,t∈N*,且m≠n,s≠t),证明;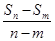 =
=  ;
;
(2)注意到(1)中Sn与n的函数关系,我们得到命题:设抛物线x2=2py(p>0)的图像上有不同的四点A,B,C,D,若xA,xB,xC,xD分别是这四点的横坐标,且xA+xB=xC+xD,则AB∥CD,判定这个命题的真假,并证明你的结论
(3)我们知道椭圆和抛物线都是圆锥曲线,根据(2)中的结论,对椭圆 +
+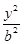 =1(a>b>0)提出一个有深度的结论,并证明之.
=1(a>b>0)提出一个有深度的结论,并证明之.
(1)已知等差数列{an}的前n项和为Sn,若m+n=s+t(m,n,s,t∈N*,且m≠n,s≠t),证明;
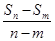 =
=  ;
;(2)注意到(1)中Sn与n的函数关系,我们得到命题:设抛物线x2=2py(p>0)的图像上有不同的四点A,B,C,D,若xA,xB,xC,xD分别是这四点的横坐标,且xA+xB=xC+xD,则AB∥CD,判定这个命题的真假,并证明你的结论
(3)我们知道椭圆和抛物线都是圆锥曲线,根据(2)中的结论,对椭圆
 +
+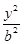 =1(a>b>0)提出一个有深度的结论,并证明之.
=1(a>b>0)提出一个有深度的结论,并证明之.见解析
(1)利用等差数列的前N项公式易证等式成立;(2)根据平行得出斜率相等,再利用两点的斜率公式推导式子成立;(3)在椭圆中利用设而不求点差法的思想得出两点斜率的关系式,从而利用斜率相等得出两直线平行
(1)设等差数列 的公差为
的公差为
 ,
,
同理: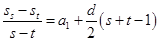 ,
, ,
,

 ;…………3分
;…………3分
(2)设 的斜率分别为
的斜率分别为 ,则
,则 ,
, ,
,
 ,
,
 ,即
,即 ;……………………………………6分
;……………………………………6分
(3)A类卷:能提出有深度的问题,并能严格证明,满分8分,如:
设椭圆 图像上有不同的四点
图像上有不同的四点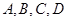 ,若线段
,若线段 的中点连线经过原点,则
的中点连线经过原点,则 .
.
证明:设: ,线段
,线段 的中点不在坐标轴上,且它们的连线经过原点,则
的中点不在坐标轴上,且它们的连线经过原点,则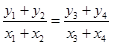 ,
,
又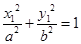 ,
,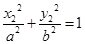 ,
,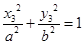 ,
,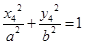
则: ,
,
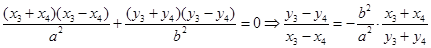 ,
,
所以: ,即
,即 ;
;
又当 中点在坐标轴上时,
中点在坐标轴上时, 同时垂直这条坐标轴,
同时垂直这条坐标轴, 成立.
成立.
B类卷:能模仿(2)提出问题,并能严格证明,满分6分,如:
椭圆 图像上有不同的四点
图像上有不同的四点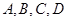 ,设它们的坐标分别是
,设它们的坐标分别是
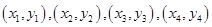 ,若
,若 ,则
,则 .
.
证明:设: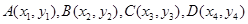 ,又
,又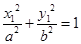 ,
,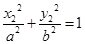 ,
,
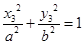 ,
,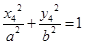
当
则: ,
,
 ,
,
所以: ,即
,即 .
.
当 时,
时, 同时垂直
同时垂直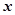 轴,
轴, 成立.
成立.
C类卷:简单模仿(2)提出问题,且不能证明,满分2分
椭圆 图像上有四点
图像上有四点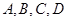 ,设它们的坐标分别是
,设它们的坐标分别是
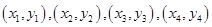 ,若
,若 ,则
,则 .
.
(1)设等差数列
 的公差为
的公差为
 ,
,同理:
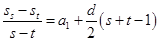 ,
, ,
,
 ;…………3分
;…………3分(2)设
 的斜率分别为
的斜率分别为 ,则
,则 ,
, ,
, ,
,
 ,即
,即 ;……………………………………6分
;……………………………………6分(3)A类卷:能提出有深度的问题,并能严格证明,满分8分,如:
设椭圆
 图像上有不同的四点
图像上有不同的四点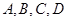 ,若线段
,若线段 的中点连线经过原点,则
的中点连线经过原点,则 .
.证明:设:
 ,线段
,线段 的中点不在坐标轴上,且它们的连线经过原点,则
的中点不在坐标轴上,且它们的连线经过原点,则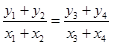 ,
,又
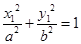 ,
,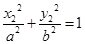 ,
,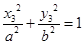 ,
,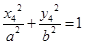
则:
 ,
,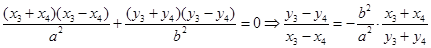 ,
,所以:
 ,即
,即 ;
;又当
 中点在坐标轴上时,
中点在坐标轴上时, 同时垂直这条坐标轴,
同时垂直这条坐标轴, 成立.
成立.B类卷:能模仿(2)提出问题,并能严格证明,满分6分,如:
椭圆
 图像上有不同的四点
图像上有不同的四点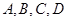 ,设它们的坐标分别是
,设它们的坐标分别是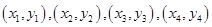 ,若
,若 ,则
,则 .
.证明:设:
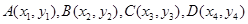 ,又
,又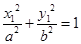 ,
,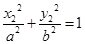 ,
,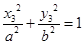 ,
,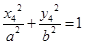
当

则:
 ,
, ,
,所以:
 ,即
,即 .
.当
 时,
时, 同时垂直
同时垂直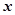 轴,
轴, 成立.
成立.C类卷:简单模仿(2)提出问题,且不能证明,满分2分
椭圆
 图像上有四点
图像上有四点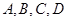 ,设它们的坐标分别是
,设它们的坐标分别是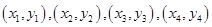 ,若
,若 ,则
,则 .
.
练习册系列答案
相关题目
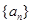 的前
的前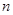 项和为
项和为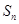 ,
,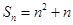 ,数列
,数列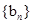 的通项公式为
的通项公式为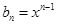 .
.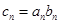 ,数列
,数列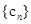 的前
的前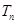 ,
,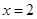 ,求数列
,求数列 的最小项的值.
的最小项的值. 中,已知
中,已知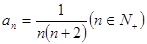 ,则
,则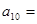 ▲ .
▲ . 是数列{
是数列{ }的前
}的前 项和,且满足
项和,且满足 则数列{
则数列{ .
. 为
为
 的各位数字之和,如
的各位数字之和,如 ,
, ,则
,则 ;记
;记 ,
, ,…,
,…, ,
, ,则
,则 = .
= .  中,
中, ,当
,当 时,
时,
 ,求数列
,求数列 的前
的前 项和
项和 .
.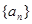 的首项为3,
的首项为3,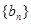 为等差数列且
为等差数列且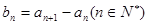 .若
.若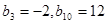 ,则
,则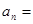 ( )
( ) 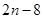
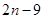
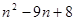
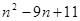
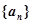 中,
中,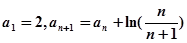 ,则数列
,则数列


