题目内容
已知圆 O:x2+y2=2交x轴正半轴于点A,点F满足 ,以F为右焦点的椭圆 C的离心率为
,以F为右焦点的椭圆 C的离心率为 .
.
(Ⅰ)求椭圆 C的标准方程;
(Ⅱ)设过圆 0上一点P的切线交直线 x=2于点Q,求证:PF⊥OQ.
解:(Ⅰ)A( ,0),F(1,0).
,0),F(1,0).
椭圆c=1,e= ,∴a=
,∴a= ,b2=a2-c2=1,
,b2=a2-c2=1,
∴椭圆D的方程为 .
.
(Ⅱ)证明:设点P(x1,y1),
过点P的圆的切线方程为y-y1= (x-x1)
(x-x1)
即y= (x-x1)+y1.
(x-x1)+y1.
由x12+y12=2得 ,
,
令x=2得 ,故点Q
,故点Q
∴KOQ= ,又KPF=
,又KPF=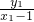 ∴KPF•KOQ=-1
∴KPF•KOQ=-1
∴PF⊥OQ.
分析:(Ⅰ)A( ,0),F(1,0).椭圆c=1,e=
,0),F(1,0).椭圆c=1,e= ,由此能求出椭圆D的方程.
,由此能求出椭圆D的方程.
(Ⅱ)设点P(x1,y1),过点P的圆的切线方程为y-y1= (x-x1),由x12+y12=2得
(x-x1),由x12+y12=2得 ,
,
令x=2得 ,故点Q
,故点Q ,由此能求出PF⊥OQ.
,由此能求出PF⊥OQ.
点评:本题考查圆锥曲线的性质和应用,解题时要注意公式的灵活运用.
 ,0),F(1,0).
,0),F(1,0).椭圆c=1,e=
 ,∴a=
,∴a= ,b2=a2-c2=1,
,b2=a2-c2=1,∴椭圆D的方程为
 .
.(Ⅱ)证明:设点P(x1,y1),
过点P的圆的切线方程为y-y1=
 (x-x1)
(x-x1)即y=
 (x-x1)+y1.
(x-x1)+y1.由x12+y12=2得
 ,
,令x=2得
 ,故点Q
,故点Q
∴KOQ=
 ,又KPF=
,又KPF=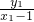 ∴KPF•KOQ=-1
∴KPF•KOQ=-1∴PF⊥OQ.
分析:(Ⅰ)A(
 ,0),F(1,0).椭圆c=1,e=
,0),F(1,0).椭圆c=1,e= ,由此能求出椭圆D的方程.
,由此能求出椭圆D的方程.(Ⅱ)设点P(x1,y1),过点P的圆的切线方程为y-y1=
 (x-x1),由x12+y12=2得
(x-x1),由x12+y12=2得 ,
,令x=2得
 ,故点Q
,故点Q ,由此能求出PF⊥OQ.
,由此能求出PF⊥OQ.点评:本题考查圆锥曲线的性质和应用,解题时要注意公式的灵活运用.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
 如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆
如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆