Question

如图，A、C两岛之间有一片暗礁，一艘小船于某日上午8时从A岛出发，以10海里/小时的速度，沿北偏东75°方向直线航行，下午1时到达B处．然后以同样的速度，沿北偏东15°方向直线航行，下午4时到达C岛．
（1）求A、C两岛之间的直线距离；
（2）求∠BAC的正弦值．

Answer 1

解（1）在△ABC中，由已知，AB=10×5=50，BC=10×3=30，
∠ABC=180°-75°+15°=120° （2分）
据余弦定理，得AC²=AB²+BC²-2AB•BCcos∠ABC
=50²+30²-2×50×30cos120°=4900，
所以AC=70．（4分）
故A、C两岛之间的直线距离是70海里．（5分）
（2）在△ABC中，据正弦定理，得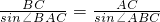，（7分）
所以．（9分）
故∠BAC的正弦值是．（10分）
分析：（1）在△ABC中，由已知，AB=10×5=50，BC=10×3=30，及∠ABC=180°-75°+15°=120可考虑利用据余弦定理求AC
（2）在△ABC中，据正弦定理，得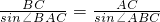可求sin∠BAC
点评：本题主要考查了利用正弦定理、余弦定理解三角形在实际问题中的应用，解题的关键是要把实际问题转化为数学问题，利用数学中的工具进行求解，试题的难度一般不大