题目内容
已知函数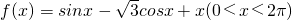 .求函数f(x)的单调区间及极值.
.求函数f(x)的单调区间及极值.
解: (0<x<2π),
(0<x<2π),
令f'(x)=0得x=π或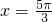 .
.
f(x)、f'(x)随x变化的情况如下表:
由表知,函数f(x)的增区间为 ,单调减区间为
,单调减区间为 .
.
f(x)的极大值为f(π)= ,f(x)的极小值为
,f(x)的极小值为 .
.
分析:求出函数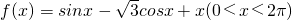 的导数,利用导数大于0求出增区间,利用导数小于0求出函数的减区间,然后列出表格,由表判断出函数的极值即可.
的导数,利用导数大于0求出增区间,利用导数小于0求出函数的减区间,然后列出表格,由表判断出函数的极值即可.
点评:本题考点是利用导数研究函数的极值,考查了求导运算及确定函数f(x)的单调区间及极值的步骤,是导数法求极值的一个基本题型.
 (0<x<2π),
(0<x<2π),令f'(x)=0得x=π或
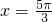 .
.f(x)、f'(x)随x变化的情况如下表:
| x | (0,π) | π |  . . |  |  |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
 ,单调减区间为
,单调减区间为 .
.f(x)的极大值为f(π)=
 ,f(x)的极小值为
,f(x)的极小值为 .
.分析:求出函数
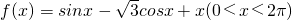 的导数,利用导数大于0求出增区间,利用导数小于0求出函数的减区间,然后列出表格,由表判断出函数的极值即可.
的导数,利用导数大于0求出增区间,利用导数小于0求出函数的减区间,然后列出表格,由表判断出函数的极值即可.点评:本题考点是利用导数研究函数的极值,考查了求导运算及确定函数f(x)的单调区间及极值的步骤,是导数法求极值的一个基本题型.

练习册系列答案
相关题目
 ),其部分图像如图所示,
),其部分图像如图所示,