Question

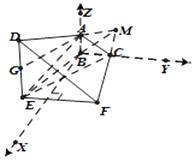
【题目】五面体ABC﹣DEF中，面BCFE是梯形，BC∥EF，面ABED⊥面BCFE，且AB⊥BE，DE⊥BE，AG⊥DE于G，若BE=BC=CF=2，EF=ED=4．
（1）求证：G是DE中点；
（2）求二面角A﹣CE﹣F的平面角的余弦．

Answer 1

【答案】
（1）证明：延长EB，FC交于M 因为M∈EB，所以M∈面AEBD M∈CF，所以M∈面CFDA

因为面AEBD与面CFDA交于DA 所以M∈DA

因为AB∥DE，BC∥EF 所以

由条件，易知四边形ABEG是矩形，所以

即G是DE中点

（2）解：作BE⊥EF于E，以 ， ， 分别为x，y，z轴构建空间直角坐标系，

所以E（ ，﹣1，0），A（0，0，2），C（O，2，O），令面AEC的法向量为 =（x，y，z），

所以 =0； =0，易得 的一个值为（ ，1，1），

因为AB垂直面BEFC，所以可令面EFC法向量为 =（0，0，1）

所以cos =

所以二面角A﹣EC﹣F的余弦值为

【解析】（1）延长EB，FC交于M，可得 M∈DA，由条件，易知四边形ABEG是矩形，所以 ，即G是DE中点（2）作BE⊥EF于E，以 ， ， 分别为x，y，z轴构建空间直角坐标系，

所以E（ ，﹣1，0），A（0，0，2），C（O，2，O），利用向量法求解