Question

【题目】已知集合

（1）判断8，9，10是否属于集合；

（2）已知集合，证明：“”的充分非必要条件是“”；

（3）写出所有满足集合的偶数.

Answer 1

【答案】（1），，；（2）详见解析；（3）所有满足集合的偶数为，．

【解析】

（1）将，，分别代入关系式，若满足关系式，则属于，若不满足关系式，则不属于，即可得答案；

（2）根据已知中集合的定义，根据集合元素与集合关系的判断，我们推证奇数可得答案；

（3）成立，当，同奇或同偶时，，均为偶数；当，一奇，一偶时，，均为奇数．由此能求出所有满足集合的偶数．

（1），，，，

假设，，则，且，

，

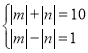，或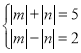，显然均无整数解，

，

，，；

（2）集合，则恒有，

，即一切奇数都属于，

又，“”的充分非必要条件是“”；

（3）集合，成立，

①当，同奇或同偶时，，均为偶数，为4的倍数；

②当，一奇，一偶时，，均为奇数，为奇数，

综上所有满足集合的偶数为，．