题目内容
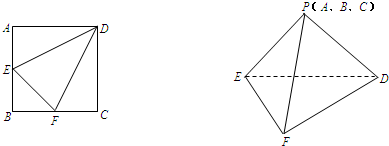
正方形ABCD中,E为AB中点,F为BC中点,将△AED、△BEF及△DCF分别沿DE、EF、DF折起,使A、B、C点重合于P点.
(1)求证:PD⊥EF;
(2)求PD与平面DEF所成角的余弦值的大小.
(1)求证:PD⊥EF;
(2)求PD与平面DEF所成角的余弦值的大小.

分析:(1)要证线线垂直常证线面垂直而利用图形折前折后的关系可得DP⊥PF,DP⊥PE然后利用线面垂直的判定定理可得DP⊥平面PEF即可得PD⊥EF.
(2)要求PD与平面DEF所成角需找到过点P且垂直于面DEF的垂线由于PE=PF,DE=DF故可取EF中点G,连DG,PG作PH⊥DG于H易证PH⊥平面DEF故PD与平面DEF所成角为∠PDG然后在Rt△PDG中求出∠PDG的余弦值即可.
(2)要求PD与平面DEF所成角需找到过点P且垂直于面DEF的垂线由于PE=PF,DE=DF故可取EF中点G,连DG,PG作PH⊥DG于H易证PH⊥平面DEF故PD与平面DEF所成角为∠PDG然后在Rt△PDG中求出∠PDG的余弦值即可.
解答:证明:(1)∵DP⊥PF,DP⊥PE
∴DP⊥平面PEF
∴PD⊥EF
(2)取EF中点G,连DG,作PH⊥DG于H
∵E、F为中点
∴△ADE≌△CDF,故DE=DF,从而DG⊥EF
同理:EF⊥PG
又PG∩DG=G
∴EF⊥平面PDG,故EF⊥PH,从而PH⊥平面DEF
∴PD与平面DEF所成角为∠PDG
设正方形ABCD边长为2,则
PD=2,DE=DF=
,EF=
,DG=
在Rt△PDG中,cos∠PDG=
=
=
∴DP⊥平面PEF
∴PD⊥EF
(2)取EF中点G,连DG,作PH⊥DG于H
∵E、F为中点
∴△ADE≌△CDF,故DE=DF,从而DG⊥EF
同理:EF⊥PG
又PG∩DG=G
∴EF⊥平面PDG,故EF⊥PH,从而PH⊥平面DEF
∴PD与平面DEF所成角为∠PDG
设正方形ABCD边长为2,则
PD=2,DE=DF=
| 5 |
| 2 |
| 3 | ||
|
在Rt△PDG中,cos∠PDG=
| PD |
| DG |
| 2 | ||||
|
2
| ||
| 3 |
点评:本题主要考查了线线垂直的证明和直线与平面所成的角的求解.解题的关键是要证线线垂直需证相面垂直这要从分利用折前折后图形间的不变关系而第二问最关键的是要找到过点P且垂直于面DEF的垂线这更要求对图形中的信息把握到位和对常用的辅助线的作法熟记于心!

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
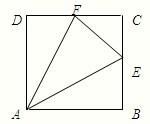 如图,正方形ABCD中,E,F分别为BC,CD的中点,设∠EAF=θ,则cosθ=
如图,正方形ABCD中,E,F分别为BC,CD的中点,设∠EAF=θ,则cosθ=
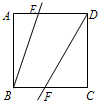 (2012•浙江模拟)如图,在正方形ABCD中,E,F分别为线段AD,BC上的点,∠ABE=20°,∠CDF=30°.将△ABE绕直线BE、△CDF绕直线CD各自独立旋转一周,则在所有旋转过程中,直线AB与直线DF所成角的最大值为
(2012•浙江模拟)如图,在正方形ABCD中,E,F分别为线段AD,BC上的点,∠ABE=20°,∠CDF=30°.将△ABE绕直线BE、△CDF绕直线CD各自独立旋转一周,则在所有旋转过程中,直线AB与直线DF所成角的最大值为