题目内容
已知| |=1,|
|=1,| |=2,
|=2, 与
与 的夹角为
的夹角为 .
.
(Ⅰ)求 •
• ;
;
(Ⅱ)向量 +λ
+λ 与向量λ
与向量λ -
- 的夹角为钝角,求实数λ的取值范围.
的夹角为钝角,求实数λ的取值范围.
解:(Ⅰ) =
=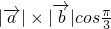 =2x1x
=2x1x =1.
=1.
(Ⅱ)( +
+ )•(λ
)•(λ -
- )=λ
)=λ 2+(λ2-1)•
2+(λ2-1)• -λ
-λ 2=λ+λ2-1-4λ=λ2-3λ-1.因为
2=λ+λ2-1-4λ=λ2-3λ-1.因为 +λ
+λ 与向量λ
与向量λ -
- 的夹角为钝角的夹角为钝角,所以(
的夹角为钝角的夹角为钝角,所以( )
)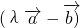 <0,令λ2-3λ-1<0,得
<0,令λ2-3λ-1<0,得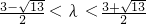 .经验证此时
.经验证此时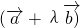 与
与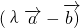 不反向.
不反向.
分析:求出两个向量的数量积;由向量的数量积公式将两个向量所成的角为钝角转化为数量积小于0且不为反向.
点评:本题考查向量的数量积公式、考查利用向量的数量积公式解决向量的夹角问题.,以及钝角的余弦值的范围,解不等式求出参数的范围
 =
=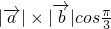 =2x1x
=2x1x =1.
=1.(Ⅱ)(
 +
+ )•(λ
)•(λ -
- )=λ
)=λ 2+(λ2-1)•
2+(λ2-1)• -λ
-λ 2=λ+λ2-1-4λ=λ2-3λ-1.因为
2=λ+λ2-1-4λ=λ2-3λ-1.因为 +λ
+λ 与向量λ
与向量λ -
- 的夹角为钝角的夹角为钝角,所以(
的夹角为钝角的夹角为钝角,所以( )
)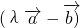 <0,令λ2-3λ-1<0,得
<0,令λ2-3λ-1<0,得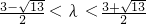 .经验证此时
.经验证此时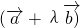 与
与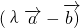 不反向.
不反向.分析:求出两个向量的数量积;由向量的数量积公式将两个向量所成的角为钝角转化为数量积小于0且不为反向.
点评:本题考查向量的数量积公式、考查利用向量的数量积公式解决向量的夹角问题.,以及钝角的余弦值的范围,解不等式求出参数的范围

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知
(xcosx+3a-b)dx=2a+6,f(t)=
(x3+ax+5a-b)dx为偶函数,则a+b=( )
| ∫ | 1 -1 |
| ∫ | t 0 |
| A、-6 | B、-12 | C、4 | D、-4 |