题目内容
请阅读下列命题:①直线y=kx+1与椭圆![]() =1总有两个交点;
=1总有两个交点;
②函数f(x)=2sin(3x-![]() )的图像可由函数f(x)=2sin3x按向量a=(-
)的图像可由函数f(x)=2sin3x按向量a=(-![]() ,0)平移得到;
,0)平移得到;
③函数f(x)=|x2-2ax+b|一定是偶函数;
④抛物线x=ay2(a≠0)的焦点坐标是(![]() ,0).
,0).
回答以上4个命题中,真命题是_______________(写出所有真命题的编号).
①④
解析:此题是多项选择题,涉及内容较多,包括圆锥曲线、三角函数、函数的性质等内容.
①法一是根据直线y=kx+1过定点(0,1),点(0,1)在椭圆![]() =1内部,所以直线y=kx+1与椭圆
=1内部,所以直线y=kx+1与椭圆![]() =1恒有两个公共点.
=1恒有两个公共点.
法二根据方程组 可得(2+k2)x2+2kx-3=0,
可得(2+k2)x2+2kx-3=0,
由△=4k2+12(2+k2)=16k2+24>0可知,方程有两根,即直线y=kx+1与椭圆![]() =1恒有两个公共点.
=1恒有两个公共点.
②设函数f(x)=2sin3x按a=(m,n)平移后得到y+n=2sin(3x+3m-![]() ),
),
令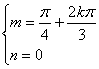 求得a=(
求得a=(![]() ,0).
,0).
③f(x)=|x2-2ax+b| ∴f(-x)=|x2+2ax+b|
∵当a=0时,f(-x)=f(x),所以为偶函数;
当a≠0时,f(-x)≠f(x),所以不为偶函数.
④x=ay2即y2=![]() x,所以抛物线焦点坐标为(
x,所以抛物线焦点坐标为(![]() ,0).
,0).

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
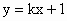 与椭圆
与椭圆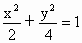 总有两个交点;
B.
总有两个交点;
B. 的图象可由f(x)=2sin3x按向量
的图象可由f(x)=2sin3x按向量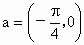 平移得到;
平移得到;
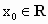 ,均有,
,均有,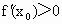 成立;
成立;
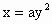 (a≠0)的焦点坐标是(
(a≠0)的焦点坐标是(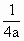 ,0).
,0).
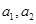 满足
满足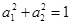 ,那么
,那么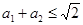 。”
。” ,因为对一切实数
,因为对一切实数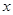 ,恒有
,恒有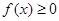 ,又
,又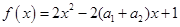 ,从而得
,从而得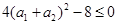 ,所以
,所以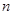 个正实数满足
个正实数满足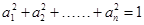 时,你可以构造函数
时,你可以构造函数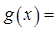 ,进一步能得到的结论为
。(不必证明)
,进一步能得到的结论为
。(不必证明)