Question

南通某地区要建造一条防洪堤，其横断面为等腰梯形，腰与底边所成角为60°（如图），考虑到防洪堤坚固性及石块用料等因素，设计其横断面要求面积为9

3

 m²，且高度不低于

3

 m．记防洪堤横断面的腰长为x（m），外周长（梯形的上底线段BC与两腰长的和）为y（m）．
（1）求y关于x的函数关系式，并指出其定义域；
（2）要使防洪堤横断面的外周长不超过10.5m，则其腰长x应在什么范围内？

Answer 1

分析：（1）如图所示，作BE⊥AD，CF⊥AD，垂足分别为E，F，则四边形BCFE为矩形，由面积公式即可得出BC用x表示式，即可得出外周长不等式及其定义域．
（2）利用（1）解出不等式，再与定义域求交集即可．

解答：解：（1）如图所示，
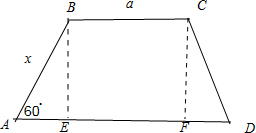设BC=a，作BE⊥AD，CF⊥AD，垂足分别为E，F，则四边形BCFE为矩形，∴EF=a，
AE=xcos60°=

1

2

x=DF，∴AD=a+x．
则高BE=xsin60°=

3

2

x≥

3

，得x≥2．
由题意得9

3

=

3 2 x(a+x+a)

2

，
得出a=

18

x

-

x

2

＞0，解得x＜6．
∴y=2x+

18

x

-

x

2

=

3x

2

+

18

x

（2≤x＜6）．
（2）∵y≤10.5，∴

3x

2

+

18

x

≤10.5，化为x²-7x+12≤0，解得3≤x≤4，
又2≤x＜6，∴3≤x≤4．
∴腰长x应在范围为[3，4]．

点评：本题考查了等腰梯形的常作的辅助线、梯形的面积公式、直角三角形的边角关系、一元二次不等式的解法，熟练掌握它们是解题的关键．