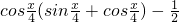Question

设函数y=f（x）满足对任意x₁、x₂∈R都有f（x₁+x₂）=f（x₁）f（x₂），且f（1）=2．
（Ⅰ）求f（2）、f（3）、f（4），猜测一个计算f（n）（n∈N^*）的公式（不要求证明）；
（Ⅱ）设an=

log2f( 1 n )

(n=1，2，3，…)，
（1）证明：a₁+a₂+a₃＞2；
（2）证明：a1+a2+a3+…+an＜2

n

(n∈N*)．

Answer 1

分析：（Ⅰ）通过赋值法x₁=x₂=1求f（2）、f（3）、f（4），得到数据表达式，猜测一个计算f（n）（n∈N^*）的公式；
（Ⅱ）根据an=

log2f( 1 n )

(n=1，2，3，…)，（1）写出a₁+a₂+a₃然后证明：a₁+a₂+a₃＞2；
（2）通过

1

n

=

2

n + n

＜

2

n + n-1

=2(

n-1

-

n

)利用放缩法证明：a1+a2+a3+…+an＜2

n

(n∈N*)．

解答：解：（Ⅰ）f（2）=2²，f（3）=2³，f（4）=2⁴（3分）
猜想f（n）=2ⁿ（4分）
（Ⅱ）（1）an=

1

n

（5分）
a₁+a₂+a₃=

1+ 1 2 + 1 3

因为

2 6 ＞1

∴

2 + 3 ＞ 6

∴

1+ 1 2 + 1 3 ＞2

a₁+a₂+a₃＞2（8分）
（2）当n=1时显然成立（9分）
当n≥2时，∵

1

n

=

2

n + n

＜

2

n + n-1

=2(

n-1

-

n

)（11分）
∴1+

1

2

+

1

3

+…+

1

n

＜2(

n

-1)＜2

n

（13分）
故对任意n∈N^*，都有a1+a2+a3+…+an＜2

n

（14分）

点评：本题是中档题，考查数列与不等式的应用，赋值法、放缩法在求值与证明中的应用，考查计算能力、推理能力．