题目内容
18.已知等边△ABC中,若$\overrightarrow{AP}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),$\overrightarrow{AQ}$=$\overrightarrow{AP}$+t$\overrightarrow{AB}$,且$\overrightarrow{AP}$⊥$\overrightarrow{AQ}$,则实数t的值为-$\frac{4}{5}$.分析 根据的加减运算法则和向量的数量积的运算法则和向量垂直的条件即可求出.
解答 解:在等边△ABC中,
∴AB=AC,∠A=60°
∵$\overrightarrow{AP}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∴$\overrightarrow{AQ}$=$\overrightarrow{AP}$+t$\overrightarrow{AB}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)+t$\overrightarrow{AB}$=($\frac{1}{3}$+t)$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$,
∵$\overrightarrow{AP}$⊥$\overrightarrow{AQ}$,
∴$\overrightarrow{AP}$•$\overrightarrow{AQ}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)•[($\frac{1}{3}$+t)$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$]=$\frac{1}{3}$($\frac{1}{3}$+t)|$\overrightarrow{AB}$|2+$\frac{1}{3}$|$\overrightarrow{AC}$|2+($\frac{4}{9}$+t)$\overrightarrow{AB}$$•\overrightarrow{AC}$,
=$\frac{1}{3}$($\frac{1}{3}$+t)|$\overrightarrow{AB}$|2+$\frac{1}{3}$|$\overrightarrow{AC}$|2+($\frac{4}{9}$+t)|$\overrightarrow{AB}$||$\overrightarrow{AC}$|•$\frac{1}{2}$=0,
∴$\frac{1}{9}$+$\frac{1}{3}$t+$\frac{1}{3}$+$\frac{2}{9}$+$\frac{1}{2}$t=0,
解得t=-$\frac{4}{5}$,
故答案为:-$\frac{4}{5}$.
点评 本题考查了加减运算法则和向量的数量积的运算法则和向量垂直的条件,属于中档题.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | $\frac{5}{4}$ | B. | -$\frac{5}{4}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
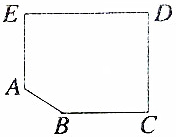 某小区内有一块荒地ABCDE,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发(如图所示),问如何设计才能使开发的面积最大?最大开发面积是多少?(已知BC=210m,CD=240m,DE=300m,EA=180m)
某小区内有一块荒地ABCDE,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发(如图所示),问如何设计才能使开发的面积最大?最大开发面积是多少?(已知BC=210m,CD=240m,DE=300m,EA=180m)