题目内容
设函数f(x)=lnx-px+1.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当p>0时,若对任意的x>0,恒有f(x)≤0,求p的取值范围.
解:(Ⅰ)∵f(x)=lnx-px+1,
∴f(x)的定义域为(0,+∞),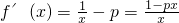 (2分)
(2分)
当p≤0时,f'(x)>0,f(x)的单调递增区间为(0,+∞)(3分)
当p>0时,令f'(x)=0,∴x= ∈(0,+∞),f'(x)、f(x)随x的变化情况如表:
∈(0,+∞),f'(x)、f(x)随x的变化情况如表: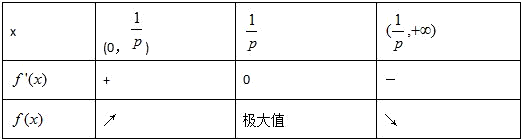
f(x)的单调递增区间为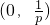 ,单调递减区间为
,单调递减区间为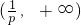 (6分)
(6分)
(Ⅱ)当p>0时在 处取得极大值
处取得极大值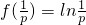 ,此极大值也是最大值,
,此极大值也是最大值,
要使f(x)≤0恒成立,只需 ,
,
∴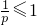 ,p≥1
,p≥1
∴p的取值范围为[1,+∞)(12分)
分析:(I)先求函数的定义域,对函数求导,分别解f′(x)>0,f′(x)<0
(II)结合(I)p>0时函数f(x)的单调性,求函数f(x)的最大值,对任意的x>0,恒有f(x)≤0?f(x)max≤0,代入求解p的取值范围.
点评:本题考查了导数的应用:求函数的单调区间,求函数的极值,在求解中不能忽略了对函数定义域的判定,当函数中含有参数时,要注意对参数的分类讨论,本题又考查了函数的恒成立问题,这也是高考在导数部分的重点考查的知识点.
∴f(x)的定义域为(0,+∞),
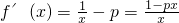 (2分)
(2分)当p≤0时,f'(x)>0,f(x)的单调递增区间为(0,+∞)(3分)
当p>0时,令f'(x)=0,∴x=
 ∈(0,+∞),f'(x)、f(x)随x的变化情况如表:
∈(0,+∞),f'(x)、f(x)随x的变化情况如表:
f(x)的单调递增区间为
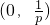 ,单调递减区间为
,单调递减区间为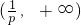 (6分)
(6分)(Ⅱ)当p>0时在
 处取得极大值
处取得极大值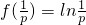 ,此极大值也是最大值,
,此极大值也是最大值,要使f(x)≤0恒成立,只需
 ,
,∴
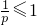 ,p≥1
,p≥1∴p的取值范围为[1,+∞)(12分)
分析:(I)先求函数的定义域,对函数求导,分别解f′(x)>0,f′(x)<0
(II)结合(I)p>0时函数f(x)的单调性,求函数f(x)的最大值,对任意的x>0,恒有f(x)≤0?f(x)max≤0,代入求解p的取值范围.
点评:本题考查了导数的应用:求函数的单调区间,求函数的极值,在求解中不能忽略了对函数定义域的判定,当函数中含有参数时,要注意对参数的分类讨论,本题又考查了函数的恒成立问题,这也是高考在导数部分的重点考查的知识点.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目