题目内容
【题目】如图，已知三棱锥
中，平面
平面ABC，
，
，BD=3，AD=1，AC=BC，M为线段AB的中点.
（Ⅰ）求证：
平面ACD；
（Ⅱ）求异面直线MD与BC所成角的余弦值；
（Ⅲ）求直线MD与平面ACD所成角的余弦值.
【答案】（Ⅰ）详见解析；（Ⅱ）
；（Ⅲ）
.
【解析】
（Ⅰ）由题意结合几何关系可得
，结合
，和线面垂直的判定定理即可证得题中的结论；
（Ⅱ）取AC中点N，连接MN，DN，易知
（或其补角）为异面直线MD与BC所成的角，据此结合几何性质可得异面直线MD与BC所成角的余弦值.
（Ⅲ）结合（Ⅱ）可知
为直线MD与平面ACD所成的角，据此可得线面角的余弦值.
（Ⅰ）∵平面
平面ABC于AB，
，
平面ABD，
∴
平面ABC，
∴，又，
，
∴
平面ACD.
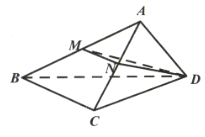
（Ⅱ）取AC中点N，连接MN，DN，
∵M是AB中点，
∴
，
∴（或其补角）为异面直线MD与BC所成的角，
由（Ⅰ）知平面ACD，
∴
平面ACD，
，
在
中，
，
，
∴
，
即异面直线MD与BC所成角的余弦值为
.
（Ⅲ）由（Ⅱ）为直线MD与平面ACD所成的角，在中，
，
∴
.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
