题目内容
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,离心率等于
轴上,离心率等于![]() ,它的一个顶点恰好在抛物线
,它的一个顶点恰好在抛物线![]() 的准线上.
的准线上.
(Ⅰ)求椭圆![]() 的标准方程.
的标准方程.
(Ⅱ)点![]() ,
,![]() 在椭圆上,
在椭圆上,![]() ,
,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.
两侧的动点.
(i)若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
(ii)当![]() ,
,![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.

【答案】(1)![]() ,(2)直线
,(2)直线![]() 的斜率为定值
的斜率为定值![]() .
.
【解析】
试题(Ⅰ)由题![]() ,得b=2,又
,得b=2,又![]() ,
,![]() ,联立计算得出即可.
,联立计算得出即可.
(Ⅱ)(i)设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,与椭圆方程联立化为
,与椭圆方程联立化为![]() ,由
,由![]() ,计算得出
,计算得出![]() , ,利用根与系数的关系可得:
, ,利用根与系数的关系可得: ![]() .四边形APBQ面积
.四边形APBQ面积![]() ,可求得面积最值.
,可求得面积最值.
(ii)由![]() ,则PA,PB的斜率互为相互数,可设直线PA的斜率为k,则PB的斜率为-k,直线PA的方程为:
,则PA,PB的斜率互为相互数,可设直线PA的斜率为k,则PB的斜率为-k,直线PA的方程为:![]() ,与椭圆的方程联立化为
,与椭圆的方程联立化为![]() ,利用根与系数的关系、斜率计算公式即可求解.
,利用根与系数的关系、斜率计算公式即可求解.
试题解析:
(Ⅰ)设椭圆![]() 的标准方程为
的标准方程为![]() ,
,
∵ 椭圆的一个顶点恰好在抛物线![]() 的准线
的准线![]() 上,
上,
∴![]() ,即
,即![]() ,
,
又∵ ![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)(i)设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
联立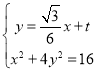 ,得
,得![]() ,
,
由![]() ,计算得出
,计算得出![]() ,
,
∴![]() ,
,![]() ,
,
∴ ![]() ,
,
∴ 四边形![]() 的面积
的面积![]() ,
,
当![]() 时,
时,![]() .
.
(ii)∵ ![]() ,则
,则![]() ,
,![]() 的斜率互为相反数,可设直线
的斜率互为相反数,可设直线![]() 的斜率为
的斜率为![]() ,
,
则![]() 的斜率为
的斜率为![]() ,直线/span>
,直线/span>![]() 的方程为:
的方程为:![]() ,
,
联立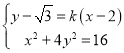 ,得
,得![]() ,
,
∴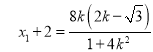 ,
,
同理可得: ,
,
∴![]() ,
,![]() ,
,
![]() ,
,
∴直线![]() 的斜率为定值
的斜率为定值![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
